ASTM E1636-94(1999)
(Practice)Standard Practice for Analytically Describing Sputter-Depth-Profile Interface Data by an Extended Logistic Function
Standard Practice for Analytically Describing Sputter-Depth-Profile Interface Data by an Extended Logistic Function
SCOPE
1.1 This practice covers a systematic method for analyzing sputter-depth-profile interface data and for accurately characterizing the shape of the interface region. Interface profile data are described with an appropriate analytic function; the parameters of this function define the interface width, its asymmetry, and its depth from the original surface. The use of this practice is recommended in order that the shapes of composition profiles of interfaces acquired with different instruments and techniques on different materials can be unambiguously compared and interpreted.
1.2 This practice is intended to be used to describe the shape of depth profile data obtained at an interface between two dissimilar materials for that case in which the measured concentration of the outer material goes from 100 to 0% and the inner material goes from 0 to 100%.
1.3 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E 1636 – 94 (Reapproved 1999)
Standard Practice for
Analytically Describing Sputter-Depth-Profile Interface Data
by an Extended Logistic Function
This standard is issued under the fixed designation E1636; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
1. Scope 3.2.1 Throughout this practice, the regions of the sigmoidal
profile will be referred to as the pre-interface, interface, and
1.1 This practice covers a systematic method for analyzing
post-interface regions. These terms are not dependent on
sputter-depth-profile interface data and for accurately charac-
whether a particular interface profile is a growth or a decay
terizing the shape of the interface region. Interface profile data
curve. The terms pre- and post- are taken in the sense of
aredescribedwithanappropriateanalyticfunction;theparam-
increasing values of the independent variable X, the sputtered
eters of this function define the interface width, its asymmetry,
depth.
anditsdepthfromtheoriginalsurface.Theuseofthispractice
is recommended in order that the shapes of composition
4. Summary of Practice
profiles of interfaces acquired with different instruments and
4.1 Sputter depth profile interface data (composition versus
techniques on different materials can be unambiguously com-
depth) is fitted to an analytic function, an extended form of the
pared and interpreted.
logistic function, in order to describe the shape of such
1.2 Thispracticeisintendedtobeusedtodescribetheshape
interface profiles. Least-squares fitting techniques are em-
of depth profile data obtained at an interface between two
ployed to determine the values of the parameters of this
dissimilar materials for that case in which the measured
extended logistic function which characterize the shape of the
concentration of the outer material goes from 100 to 0% and
interface. Interface width, depth, and asymmetry are deter-
the inner material goes from 0 to 100%.
mined by these parameters.
1.3 This standard does not purport to address all of the
safety concerns, if any, associated with its use. It is the
5. Significance and Use
responsibility of the user of this standard to establish appro-
5.1 Information on interface composition is frequently ob-
priate safety and health practices and determine the applica-
tained by measuring surface composition while the specimen
bility of regulatory limitations prior to use.
material is gradually removed by ion bombardment (see Guide
E1127 and Practice E1162). In this way, interfaces are
2. Referenced Documents
revealedandcharacterizedbythemeasurementofcomposition
2.1 ASTM Standards:
2 versus depth to obtain a sputter-depth profile. The shape of
E 673 Terminology Relating to Surface Analysis
such interface profiles contains information about the physical
E 1127 Guide for Depth Profiling in Auger Electron Spec-
2 and chemical properties of the interface region. In order to
troscopy
accurately and unambiguously describe this interface region
E1162 PracticeforReportingSputterDepthProfileDatain
2 and to determine its width (see Guide E1438), it is necessary
Secondary Ion Mass Spectrometry (SIMS)
to define the shape of the entire interface profile with a single
E1438 GuideforMeasuringWidthsofInterfacesinSputter
2 analytic function.
Depth Profiling Using SIMS
5.2 Although no general physical model currently exists for
3. Terminology describing the shape of interface sputter-depth profiles, inter-
face profiles do have a sigmoidal shape characteristic of the
3.1 Definitions—For definitions of terms used in this prac-
cumulativelogisticdistribution.Useofsuchalogisticfunction
tice, see Terminology E673.
is physically plausible and is superior to other functions (for
3.2 Definitions of Terms Specific to This Standard:
example, polynomials) that have heretofore been used for
This practice is under the jurisdiction of ASTM Committee E-42 on Surface
Analysis and is the direct responsibility of Subcommittee E42.08 on Ion Beam
Sputtering. Kirchhoff,W. H., Chambers, G. P., and Fine, J., “AnAnalytical Expression for
Current edition approved Sept. 15, 1994. Published November 1994. Describing Auger Sputter Depth Profile Shapes of Interfaces,” Journal of Vacuum
Annual Book of ASTM Standards, Vol 03.06. Science and Technology, , p. 1666, 1986.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
E 1636
interface profile analysis in that it contains the minimum fit requires an iterative solution. Consequently, Y, as expressed
number of parameters for describing interface shapes. by Eq 3 , can be expanded in a Taylor series about the current
5.3 Manyattemptshavebeenmadetocharacterizeinterface values of the parameters and the Taylor series terminated after
profiles with general functions (such as polynomials or error the first (that is, linear) term for each parameter. Y (obs)− Y
functions) but these have suffered from instabilities and an (calc) is fit to this linear expression and the least-squares
inabilitytohandlepoorlystructureddata.Choiceofthelogistic routine returns the corrections to the parameters. The param-
function along with a specifically written least-squares proce- eters are updated and the procedure is repeated until the
dure (described in Appendix X1) can provide statistically corrections to the parameters are deemed to be insignificant
evaluated parameters that describe the width, asymmetry, and compared to their standard deviations. Values for interface
depth of interface profiles in a reproducible and unambiguous width, depth, and asymmetry can be calculated from the
way. parameters of the fitted logistic function.
6.3 Implementation of this procedure can be readily accom-
6. Description of the Analysis
plishedbymakinguseofaspecializedcomputeralgorithmand
6.1 Logistic Function Data Analysis—In its simplest form, supporting software (LOGIT) developed specifically for this
the logistic function may be written as: application and described in Appendix X1.
7. Interpretation of Results
Y 5 (1)
2x
1 1 e
7.1 The seven parameters necessary to characterize the
inwhich Yprogressesfrom0to1as Xvariesfrom−`to+`.
interface profile shape are determined by a least-squares fit of
The differential equation generating this function is:
the interface data to the extended logistic function. These
parameters are related to the three distinct regions of the
dY/dX 5 Y 1 2 Y (2)
~ !
interface profile. Two parameters, an intercept A and a slope
and in this form describes a situation where a measurable
A arenecessarytodefinethepre-interfaceasymptotewhiletwo
s
quantity Y grows in proportion to Y and in proportion to finite
more, B and B , define the post-interface asymptote. For the
s
resources required by Y. The logistic function was first named
analysis of typical interface profiles, it is usual to assume that
and applied to population growth in the last century by
both of these slopes are zero.Two more parameters, D and X ,
4 o o
Verhulst. The logistic function as a distribution function and
define the slope and position of the transition region. In
growth curve has been extensively reviewed by Johnson and
addition, an asymmetry parameter Q that causes the width
Kotz. Interfaceprofiledataisfittedtoanextendedformofthe
parameter to vary logistically from O to 2D , is introduced as
o
logistic function:
a measure of the difference in curvature in the pre- and
z
Y 5 @A 1 A ~X 2 X !#/~1 1 e !
post-transition ends of the transition region. If Q < O, the
s o
2z
1 @B 1 B ~X 2 X !#/~1 1 e ! (3)
pre-transition region has the greatest (sharpest) curvature. If Q
s o
> O, the post-transition region has the greatest curvature. If
where:
Q 5O, D 5 D and the transition profile is symmetric. The
o
z 5 ~X 2 X !/D (4)
o
parameter Q has the dimensions of 1/X whereas D has the
o
and:
dimensions of X. The product QD is dimensionless and is a
o
Q~X2X ! measure of the asymmetry of the profile independent of its
o
D 52 D / 1 1 e (5)
@ #
o
width. If the absolute magnitude of QD is less than 0.1, the
o
6.1.1 Y is a measure of the elemental surface concentration
asymmetry in the transition profile should be barely discern-
of one of the components and X, the independent variable, is a
ible.
measure of the sputtered depth, usually expressed as a sputter-
7.2 The final results should include the calculated values of
ing time. Pre-interface and post-interface elemental surface
Y and associated statistics, the values of the determined
concentrations are described by the parameters A and B,
parameters and their uncertainties, and statistics related to the
respectively,theparametersA andB areintroducedtoaccount
s s
overall quality of the least-squares fit.
for time dependent instrumental effects. X is the midpoint of
o
7.3 The width of the interface region, I, is the depth (time)
f
theinterfaceregion(interfacedepthortime).Thescalingfactor
required for the decay or growth curve to progress from a
D is the characteristic depth for sputtering through the
o
fraction f of completion to (1− f) of completion. For the case
interface region; Q, an asymmetry parameter, is a measure of
where Q 5O, I is proportional to D and is given by the
f o
thedifferenceincurvatureinthepre-andpost-interfaceendsof
simple formula:
theinterfaceregion.Allmeasuresoftheinterfacewidthcanbe
I 52 D 1n @~1 2 f!/f# (6)
f o
determined from D and Q.
o
6.2 Fitting of interface profile data to the above functions, so that, for example, the traditional 16 to 84% interface
Eq 3 , can be accomplished by using least-squares techniques. width is 3.32 D .
o
Because these equations are non-linear functions of the three 7.4 Introduction of the asymmetry parameter Q into the
transition-region parameters, X , D , and Q, the least-squares extended logistic function makes the calculation of the 16 to
o o
84% points of the interface more complicated. In particular,
for fractions f and (1− f) of completion of the interface
Verhulst, P. F., Acad. Brux. Vol 18, p. 1, 1845.
transition:
Johnson,N.L.andKotz,S.,“DistributionsinStatistics:ContinuousUnivariate
Q X 2X !
~
f o
Distributions,” Houghton Mifflin Co., Boston, 2, Chapter 22, 1970. X 5 X 12 D 1n @f/~1 2 f!#/@1 1 e # (7)
f o o
E 1636
and:
Q~X 2X !
12f o
X 5 X 12 D 1n @~1 2 f!/f#/@1 1 e # (8)
~12f! o o
X and X can be evaluated most readily by Newton’s
f (1−f)
method of successive approximations.
8. Reporting of Results
8.1 Interface profile shapes can be accurately characterized
bytheextendedlogisticfunctionanditsparameters.Resultsof
such interface analysis should report these parameters (X , D ,
o o
Q) together with their uncertainties, the standard deviation of
the fit, and an interface width obtained from D and Q that is
o
based on some accepted definition (for example, 16 to 84%
concentration change).
8.2 Sputtereddepth, X,isoftendifficulttodetermineexperi-
mentally so that depth profile data are normally acquired with
time as the independent variable. This sputtered time can be
referenced with respect to a removal time obtained with a
calibrated sputtering standard under the same sputtering con-
ditions of ion energy, beam angle, current density, etc. as the
interface measurement itself. In this way, time can be trans-
formed into an equivalent depth derived from a standard
material and this equivalent depth should be used in reporting
the interface parameters and analysis results. Sputtering stan-
dardsareavailablefromtheNationalInstituteofStandardsand
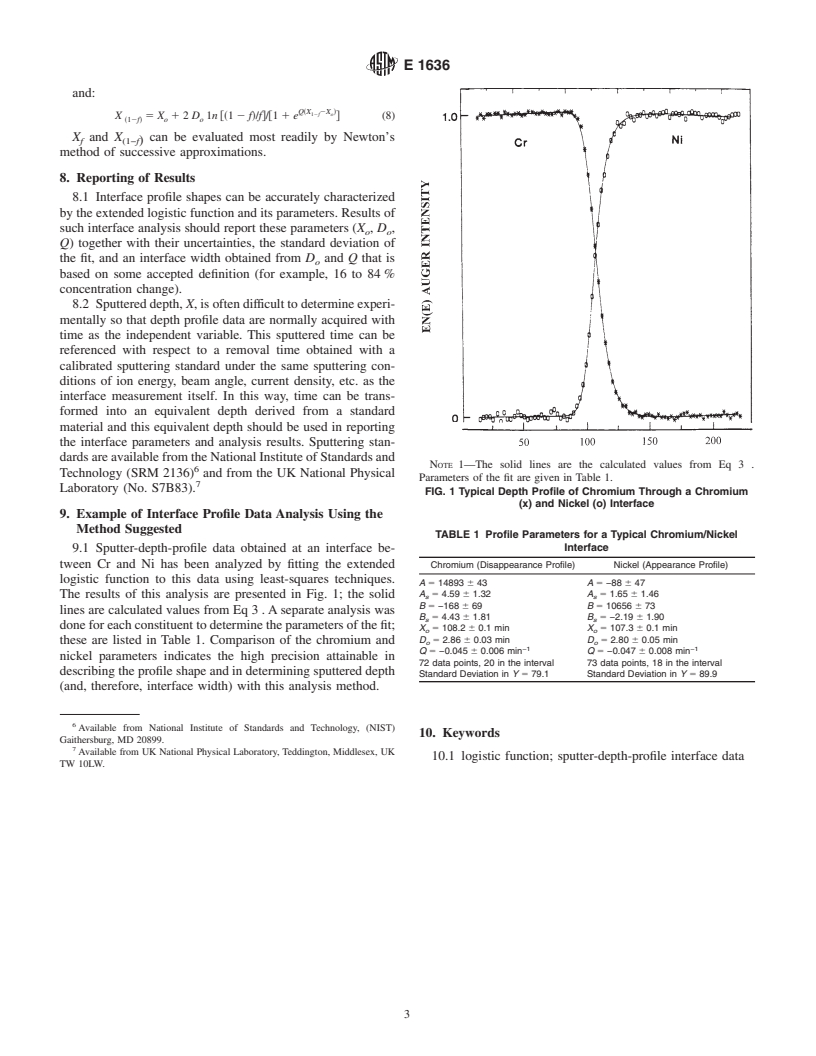
NOTE 1—The solid lines are the calculated values from Eq 3 .
Technology (SRM 2136) and from the UK National Physical
Parameters of the fit are given in Table 1.
Laboratory (No. S7B83).
FIG. 1 Typical Depth Profile of Chromium Through a Chromium
(x) and Nickel (o) Interface
9. Example of Interface Profile Data Analysis Using the
Method Suggested
TABLE 1 Profile Parameters for a Typical Chromium/Nickel
Interface
9.1 Sputter-depth-profile data obtained at an interface be-
tween Cr and Ni has been analyzed by fitting the extended
Chromium (Disappearance Profile) Nickel (Appearance Profile)
logistic function to this data using least-squares techniques.
A 5 14893 6 43 A 5 −88 6 47
A 5 4.59 6 1.32 A 5 1.65 6 1.46
The results of this analysis are presented in Fig. 1; the solid
s s
B 5 −168 6 69 B 5 10656 6 73
lines are calculated values from Eq 3 .Aseparate analysis was
B 5 4.43 6 1.81 B 5 −2.19 6 1.90
s s
doneforeachconstituenttodeterminetheparametersofthefit;
X 5 108.2 6 0.1 min X 5 107.3 6 0.1 min
o o
D 5 2.86 6 0.03 min D 5 2.80 6 0.05 min
these are listed in Table 1. Comparison of the chromium and o o
−1 −1
Q 5 −0.045 6 0.006 min Q 5 −0.047 6 0.008 min
nickel parameters indicates the high precision attainable in
72 data points, 20 in the interval 73 data points, 18 in the interval
describingtheprofileshapeandindeterminingsputtereddepth
Standard Deviation in Y 5 79.1 Standard Deviation in Y 5 89.9
(and, therefore, interface width) with this analysis method.
Available from National Institute of Standards and Technology, (NIST)
10. Keywords
Gaithersburg, MD 20899.
Available from UK National Physical Laboratory, Teddington, Middlesex, UK
10.1 logistic function; sputter-depth-profile interface data
TW 10LW.
E 1636
APPENDIX
(Nonmandatory Information)
X1. FITTING OF DEPTH PROFILE INTERFACE DATA TO THE LOGISTIC FUNCTION BY MEANS OFA
SPECIALIZED COMPUTER ALGORITHM, LOGIT
X1.1 Scope X1.4 Description of the Fitting Procedure Used in
LOGIT
X1.1.1 This appendix describes a specialized computer
algorithm and supporting software (LOGIT) developed for the X1.4.1 Data in the form of X, Y pairs and saved in a file are
fit by the method of least-squares to the following equation:
fitting of depth profile interface data to the extended logistic
function in order to determine the parameters of this fitted
z
Y 5 A 1 A X 2 X / 1 1 e
@ ~ !# ~ !
s o
function. These parameters characterize the shape of the
2z
1 @B 1 B ~X 2 X !#/~1 1 e ! (X1.1)
s o
interface region and so define the interface width, its asymme-
where:
try, and its depth from the original surface.
Q~X2X !
o
z 5 ~X 2 X !/D,and D 52D /@1 1 e # (X1.2)
o o
X1.2 Significance and Use
X1.4.1.1 Because these equations are non-linear functions
X1.2.1 LOGIT has been developed to fit interface profile
of the three transition region parameters, X , D , and Q, the
o o
data to the extended logistic function. The specifically written
least-squaresfitrequiresaniterativesolution.Consequently, Y,
least-squares procedure used in LOGIT
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.