ASTM E2865-12

Standard Guide for Measurement of Electrophoretic Mobility and Zeta Potential of Nanosized Biological Materials

SCOPE
1.1 This guide deals with the measurement of mobility and zeta potential in systems containing biological material such as proteins, DNA, liposomes and other similar organic materials that possess particle sizes in the nanometer scale (100 nm).
1.2 The values stated in SI units are to be regarded as standard. No other units of measurement are included in this standard.
1.3 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.

General Information

• Status: Historical
• Publication Date: 31-Dec-2011
• ICS: 07.120 - Nanotechnologies
• Technical Committee: E56 - Nanotechnology
• Drafting Committee: E56.02 - Physical and Chemical Characterization

Standards Content (Sample)

NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E2865 − 12
Standard Guide for
Measurement of Electrophoretic Mobility and Zeta Potential
of Nanosized Biological Materials
This standard is issued under the fixed designation E2865; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope ISO 13321Particle Size Analysis — Photon Correlation
Spectroscopy
1.1 This guide deals with the measurement of mobility and
zetapotentialinsystemscontainingbiologicalmaterialsuchas
3. Terminology
proteins, DNA, liposomes and other similar organic materials
that possess particle sizes in the nanometer scale (<100 nm). 3.1 Definitions—Definitions of nanotechnology terms can
be found in Terminology E2456.
1.2 The values stated in SI units are to be regarded as
3.2 Definitions of Terms Specific to This Standard:
standard. No other units of measurement are included in this
3.2.1 Brownian motion—is the random movement of par-
standard.
ticles suspended in a fluid caused by external bombardment by
1.3 This standard does not purport to address all of the
dispersant atoms or molecules.
safety concerns, if any, associated with its use. It is the
3.2.2 dielectric constant—the relative permittivity of a ma-
responsibility of the user of this standard to establish appro-
terialforafrequencyofzeroisknownasitsdielectricconstant
priate safety and health practices and determine the applica-
(or static relative permittivity).
bility of regulatory limitations prior to use.
1.4 This international standard was developed in accor-
3.2.2.1 Discussion—Technically,itistheratiooftheamount
dance with internationally recognized principles on standard- of electrical energy stored in a material by an applied voltage,
ization established in the Decision on Principles for the
relative to that stored in a vacuum.
Development of International Standards, Guides and Recom-
3.2.3 electrophoretic mobility—the motion of dispersed par-
mendations issued by the World Trade Organization Technical
ticlesrelativetoafluidundertheinfluenceofanelectricalfield
Barriers to Trade (TBT) Committee.
(usually considered to be uniform).
3.2.4 isoelectric point—point of zero electrophoretic mobil-
2. Referenced Documents
2 ity.
2.1 ASTM Standards:
E1470 Test Method for Characterization of Proteins by 3.2.5 mobility—see electrophoretic mobility.
Electrophoretic Mobility
3.2.6 redox reaction—a chemical reaction in which atoms
E2456Terminology Relating to Nanotechnology
have their oxidation number (oxidation state) changed.
2.2 ISO Standards:
3.2.7 stability—the tendency for a dispersion to remain in
ISO 13099-1 Colloidal systems — Methods for zeta-
the same form for an appropriate timescale (for example, the
potential determination — Part 1: Electroacoustic and
experiment duration; on storage at 358K).
electrokinetic phenomena
3.2.7.1 Discussion—In certain circumstances (for example
ISO 13099-2 Colloidal systems — Methods for zeta-
water colloid flocculation) instability may be the desired
potential determination — Part 2: Optical methods
property.
3.2.8 van der Waals forces—in broad terms the forces
This guide is under the jurisdiction of ASTM Committee E56 on Nanotech-
between particles or molecules.
nology and is the direct responsibility of Subcommittee E56.02 on Physical and
3.2.8.1 Discussion—These forces tend to be attractive in
Chemical Characterization.
Current edition approved Jan. 1, 2012. Published June 2012. DOI: 10.1520/
nature (because such attractions lead to reduced energy in the
E2865-12.
system) unless specific steps are undertaken to prevent this
For referenced ASTM standards, visit the ASTM website, www.astm.org, or
attraction.
contact ASTM Customer Service at [e-mail]. For Annual Book of ASTM
Standards volume information, refer to the standard’s Document Summary page on
3.2.9 zeta potential—the potential difference between the
the ASTM website.
dispersion medium and the stationary layer of fluid attached to
Available from International Organization for Standardization (ISO), 1, ch. de
la Voie-Creuse, CP 56, CH-1211 Geneva 20, Switzerland, http://www.iso.org. the dispersed particle.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
E2865 − 12
3.2.10 zwitterionic—a molecule with a positive and a nega- movement may be hindered. In this circumstance, although a
tive electrical charge. movement can be detected and measured, it may provide
3.2.10.1 Discussion—Amino acids are the best known ex-
interpretation issues when a conversion to zeta potential is
amples of zwitterions.
attempted.
4.3.3 Zeta potential tends only to be important in the sub-5
4. Summary of Practice
µm (and thus relevant to the sub-100 nm region considered in
4.1 Introduction—It is not the intention of this guide to
this text) region where van der Waals attractive forces are of a
spend any significant time on the theory of zeta potential and
similar order of magnitude as inertial forces. Thus if sedimen-
the routes by which a particle acquires charge within a system.
tation (function of size and density of the particle with respect
Indeed it may be more appropriate to deal only with the
to the medium it resides) is occurring or has occurred, the
movement or mobility of particles under an electrical field
system is clearly not ideal for a zeta potential or mobility
where conversion to zeta potential is not even attempted. The
measurement. With significant settling the measurement of
relevant text books (for example, see Hunter (1) ) should be
mobility is obviously compromised. The lower limit for
consulted along with the more academic ISO references (ISO
measurement of electrophoretic mobility is in effect deter-
13099-1 and ISO 13099-2). The IUAPC report (2) is also very
mined by the signal to noise which is a complex function of
useful, albeit fairly theoretical, but it does contain a section
size, concentration and relative refractive index of the particu-
(4.1.2) entitled ‘How and under which conditions the electro-
late system. An unambiguous statement of the lower size is
phoretic mobility can be converted into ζ-potential’. The
therefore not possible.
Corbett and Jack paper (3) contains excellent practical advice
4.3.4 Zeta potential and its (assumed) relation to system
for measurement of protein mobility and is recommended.
stability are reasonably well understood in aqueous systems.
4.2 Test Method E1470 is based around a sole vendor’s
The classic examples are indicated in Thomas Riddick’s text
equipment, but this does not deal with the basis of the
(4). The obvious or stated link with formulation or product
measurement or provide guidance in the practice of the
stability is not obvious for organic media where the counter-
measurement. It is one intention of this guide to address those
ions will be strongly bound to the particle surface and the
deficits.
position of the diffuse layer will be difficult to identify in an
4.3 The following aspects need emphasis:
(effectively) insulating external medium. Again, what is often
4.3.1 Zetapotentialisafunctionoftheparticulatesystemas
forgotten, is that conductivity is required in the ‘background’
-1
a whole – so the environment that the particle resides in (pH,
solution (typically 0.001 molL sodium chloride (NaCl) is
concentration, ionic strength, polyvalent ions) will directly
utilized) so that an electrical field can be correctly applied
influence the magnitude and, in certain circumstances, the sign
without effects such as electrode polarization (causing voltage
of the acquired charge. In particular, small quantities (parts per
irregularities) occurring. Mobility or zeta potential measure-
2+
million) of polyvalent ions (for example calcium ions (Ca ),
ments should not be made in de-ionized water. In non-polar
3+
iron(III)ions(Fe ))orotherimpuritiescansignificantlyaffect
dispersant liquids, conversion of observed mobility to zeta
the magnitude of the zeta potential. It is obvious, but often
potential may need some understanding of the position and
ignored, that there is no such concept of the zeta potential of a
thickness (single atom or molecule?) of the double layer, but
powder.
this is not relevant to measurements in (aqueous) biological
4.3.2 The calculation of zeta potential from mobility mea-
media.
surement typically refers to the unrestricted mobility of a
4.3.5 Itismobility(movement)thatisusuallymeasuredand
particle in suspension. In crowded environments (that is high
the conversion to zeta potential relies on application of the
concentration) particle-particle interactions occur and the
Henry equation. (See also Fig. 1).
4 εζ f~κα!
The boldface numbers in parentheses refer to a list of references at the end of
U 5 (1)
E
6πη
this standard.
FIG. 1 Equation (1)
E2865 − 12
where: et al. (6)). 1/κ can be envisioned as the "thickness" of the
electrical double layer (the Debye length) and thus the units of
U = the electrophoretic mobility (measured by
E
κarereciprocallength.Thusf(κα)isdimensionlessandusually
instrument),
assignedthevalue1.00or1.50.Forparticlesinpolarmediathe
ε = the dielectric constant of the dispersion medium,
maximum value of f(κα) is taken to be 1.5 (Smoluchowski
ζ = the (calculated) zeta potential,
f(κα) = Henry’s function (see below), and
approximation) and for particles in non-polar media the mini-
η = theviscosityofthemedium(measuredorassumed).
mum value of f(κα) is 1 (Hückel approximation). It is the
former that we are considering in this text. The literature does
4.3.5.1 Itisimportanttospecifytheunitsofmeasurementas
indicate intermediate values for f(κα) but in most biologically
failure to get these correct will lead incompatibility of units on
relevant media the value of 1.5 is the most appropriate.
the right and left hand side of the above equation. The normal
4.3.5.4 In terms of viscosity, η, the SI physical unit of
SI units (metre, kilogram, second) are not often utilized in this
dynamic viscosity is the pascal-second (Pa·s), (equivalent to
area as they are too large for practical purposes (diffusion
N·s/m , or kg/(m·s)). Water at 293K has a viscosity of
distances of one metre are not routinely encountered!) — see
0.001002 Pa·s. The cgs physical unit for dynamic viscosity is
additional unit information in Ref. (5). We need to remember
the poise (P). It is more commonly expressed, particularly in
that the mobility and diffusion coefficient are a flux (and thus
ASTM standards, as centipoise (cP). Water at 293K has a
area) per unit time. The mobility will be scaled by the field
viscosity of 1.0020 cP.
(volts/distance). Ref. (5) recommended units for electropho-
2 -1 -1 -1
retic mobility are m s V . This can be expressed as (ms )/
NOTE 1—At room temperature (assumed 298K) in water, all of the
-1
(Vm ) or a velocity per unit field. In practice, the electropho- expressions are constants except for the (measured) mobility and the
equation defers to:
retic mobility, U , has more convenient units of µm /Vs Often
E
mobilities are expressed in confused units (for example, the
Zetapotential 5 K*electrophoreticmobility, U ; 12.85*U (2)
E E
-1
oft-utilized µmcm /Vs because this gives rise to mobility
where the value of K (collective proportionality constant) is ~12.85 if
thezetapotentialistobestatedinmVandthisfallsoutnaturallyfromthe
values in the convenient 610 region). Mobilities expressed
-1
Henry equation if the deprecated µmcm /Vs unit is used for electropho-
with a negative sign imply a negative zeta potential.
retic mobility.
4.3.5.2 ε is the dielectric constant of the dispersion medium
dimensionless/nounitsasitisaratiooftherelativepermittivity 4.3.5.5 As well as movement under the constraint of an
ofthematerialtovacuumwhoserelativepermittivityisdefined electric field, some degree of Brownian motion will also occur
as 1. and may need to be considered. In biological media of
4.3.5.3 f(κα) is usually referred to as “Henry’s function” relatively high ionic strength the Hückel model (f(κα)=1)for
where α is the radius of the particle. κ is referred to as the zetapotentialcalculationisinappropriateandthevalueoff(κα)
Debye parameter and can be calculated from the electronic should be calculated from the measured size and the known
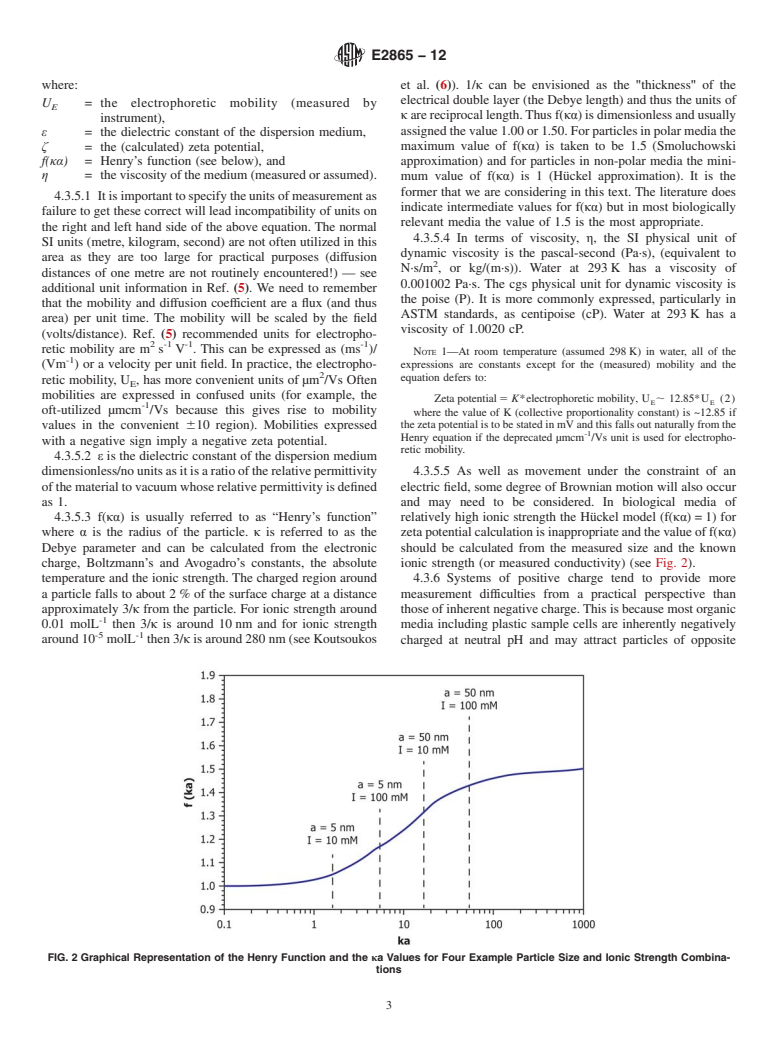
charge, Boltzmann’s and Avogadro’s constants, the absolute ionic strength (or measured conductivity) (see Fig. 2).
temperature and the ionic strength. The charged region around 4.3.6 Systems of positive charge tend to provide more
a particle falls to about 2% of the surface charge at a distance measurement difficulties from a practical perspective than
approximately 3/κ from the particle. For ionic strength around thoseofinherentnegativecharge.Thisisbecausemostorganic
-1
0.01 molL then 3/κ is around 10nm and for ionic strength media including plastic sample cells are inherently negatively
-5 -1
around10 molL then3/κisaround280nm(seeKoutsoukos charged at neutral pH and may attract particles of opposite
FIG. 2 Graphical Representation of the Henry Function and the κa Values for Four Example Particle Size and Ionic Strength Combina-
tions
E2865 − 12
charge removing them from suspension and altering the wall measure a few µLof sample with specific experimental set-ups
potential. It is useful to have some form of automation for pH as the electrodes need to be of a finite size and distance apart.
adjustment – for example a titrator. This eases the adjustment In many instances a few millilitres of solution or suspension
of pH and additive concentration. will make life easy, especially if flushing of a cell is needed,
but this is not always available. If the material can be held as
4.3.7 It is of no value to state a zeta potential value without
a ‘plug’ it may be possible to work with considerably less
description of the manner in which it was measured together
quantity.
with vital measurement parameters. Zeta potential without a
4.4.4 Biological material is often contained in buffered
stated pH, ionic compostion, and electrolyte concentration
solutions of relatively high ionic concentration. For example,
value is close to meaningless.
phosphate buffered saline (PBS) is constituted of 0.0032
4.4 Biological Molecules and Entities—Again, a few obvi-
-1
molL disodium hydrogen phosphate (Na HPO ), 0.005
2 4
ous points will need mentioning:
-1 -1
molL monopotassium phosphate (KH PO , 0.0013 molL
2 4
4.4.1 Many materials such as proteins contain charges and -1
potassium chloride (KCl), 0.135 molL NaCl, and
...