ASTM E598-96(2002)
(Test Method)Standard Test Method for Measuring Extreme Heat-Transfer Rates from High-Energy Environments Using a Transient, Null-Point Calorimeter
Standard Test Method for Measuring Extreme Heat-Transfer Rates from High-Energy Environments Using a Transient, Null-Point Calorimeter
SCOPE
1.1 This test method covers the measurement of the heat-transfer rate or the heat flux to the surface of a solid body (test sample) using the measured transient temperature rise of a thermocouple located at the null point of a calorimeter that is installed in the body and is configured to simulate a semi-infinite solid. By definition the null point is a unique position on the axial centerline of a disturbed body which experiences the same transient temperature history as that on the surface of a solid body in the absence of the physical disturbance (hole) for the same heat-flux input.
1.2 Null-point calorimeters have been used to measure high convective or radiant heat-transfer rates to bodies immersed in both flowing and static environments of air, nitrogen, carbon dioxide, helium, hydrogen, and mixtures of these and other gases. Flow velocities have ranged from zero (static) through subsonic to hypersonic, total flow enthalpies from 1.16 to greater than 4.65 x 101 MJ/kg (5 x 10 2 to greater than 2 x 104 Btu/lb.), and body pressures from 105 to greater than 1.5 x 10 7 Pa (atmospheric to greater than 1.5 x 10 2 atm). Measured heat-transfer rates have ranged from 5.68 to 2.84 x 10 2 MW/m2 (5 x 102 to 2.5 104 Btu/ft2-sec).
1.3 The most common use of null-point calorimeters is to measure heat-transfer rates at the stagnation point of a solid body that is immersed in a high pressure, high enthalpy flowing gas stream, with the body axis usually oriented parallel to the flow axis (zero angle-of-attack). Use of null-point calorimeters at off-stagnation point locations and for angle-of-attack testing may pose special problems of calorimeter design and data interpretation.
1.4 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E 598 – 96 (Reapproved 2002)
Standard Test Method for
Measuring Extreme Heat-Transfer Rates from High-Energy
Environments Using a Transient, Null-Point Calorimeter
This standard is issued under the fixed designation E 598; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
1. Scope 2. Referenced Documents
1.1 This test method covers the measurement of the heat- 2.1 ASTM Standards:
transfer rate or the heat flux to the surface of a solid body (test E 422 Test Method for Measuring Heat Flux Using a
sample) using the measured transient temperature rise of a Water-Cooled Calorimeter
thermocouple located at the null point of a calorimeter that is E 511 Test Method for Measuring Heat Flux Using a
installed in the body and is configured to simulate a semi- Copper-Constantan Circular Foil, Heat-Flux Gage
infinite solid. By definition the null point is a unique position
3. Terminology
on the axial centerline of a disturbed body which experiences
3.1 Symbols:
the same transient temperature history as that on the surface of
a solid body in the absence of the physical disturbance (hole)
for the same heat-flux input.
a = Radius of null-point cavity, m (in.)
1.2 Null-point calorimeters have been used to measure high
b = Distance from front surface of null-point calorimeter
convective or radiant heat-transfer rates to bodies immersed in
to the null-point cavity, m (in.)
both flowing and static environments of air, nitrogen, carbon
C = Specific heat capacity, J/kg–K (Btu/lb-°F)
p
dioxide, helium, hydrogen, and mixtures of these and other
d = Diameter of null-point cavity, m (in.)
gases. Flow velocities have ranged from zero (static) through
k = Thermal conductivity, W/m–K (Btu/in.-sec-°F)
subsonic to hypersonic, total flow enthalpies from 1.16 to
L = Length of null-point calorimeter, m (in.)
1 2
greater than 4.65 3 10 MJ/kg (5 3 10 to greater than
q = Calculatedormeasuredheatfluxorheat-transfer-rate,
4 5
2 2
2 3 10 Btu/lb.), and body pressures from 10 to greater than
W/m (Btu/ft -sec)
7 2
1.5 3 10 Pa (atmospheric to greater than 1.5 3 10 atm).
q = Constant heat flux or heat-transfer-rate, W/m (Btu/
Measured heat-transfer rates have ranged from 5.68 to
ft -sec)
2 2 2 4 2
2.84 3 10 MW/m (5 3 10 to 2.5 3 10 Btu/ft -sec).
R = Radial distance from axial centerline of TRAX ana-
1.3 The most common use of null-point calorimeters is to
lytical model, m (in.)
measure heat-transfer rates at the stagnation point of a solid r = Radial distance from axial centerline of null-point
bodythatisimmersedinahighpressure,highenthalpyflowing cavity, m (in.)
T = Temperature, K (°F)
gas stream, with the body axis usually oriented parallel to the
T = Temperature on axial centerline of null point, K (°F)
flow axis (zero angle-of-attack). Use of null-point calorimeters
b
T = Temperature on surface of null-point calorimeter, K
at off-stagnation point locations and for angle-of-attack testing s
(°F)
may pose special problems of calorimeter design and data
t = Time, sec
interpretation.
Z = DistanceinaxialdirectionofTRAXanalyticalmodel,
1.4 This standard does not purport to address all of the
m (in.)
safety concerns, if any, associated with its use. It is the
2 2
a = Thermal diffusivity, m /sec (in. /sec)
responsibility of the user of this standard to establish appro-
3 3
r = Density, kg/m (lb/in. )
priate safety and health practices and determine the applica-
bility of regulatory limitations prior to use.
4. History of Test Method
4.1 FromliteraturereviewsitappearsthatMastersandStein
(1) werethefirsttodocumenttheresultsofananalyticalstudy
This test method is under the jurisdiction of ASTM Committee E21 on Space
Simulation andApplications of Space Technology and is the direct responsibility of
Subcommittee E21.08 on Thermal Protection. Annual Book of ASTM Standards, Vol 15.03.
Current edition approved Oct. 10, 1996. Published December 1996. Originally The boldface numbers in parentheses refer to the list of references at the end of
e1
published as E 598 – 77. Last previous edition E 598 – 77 (1990). this test method.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
E 598
of the temperature effects of axial cavities drilled from the Beck and Hurwicz computed errors due to relatively large
backsideofawallwhichisheatedonthefrontsurface(seeFig. thermocouplewiresintheaxialcavityandwereabletosuggest
1). These investigators were primarily concerned with the
that the optimum placement of the thermocouple in the cavity
deviation of the temperature measured in the bottom of the
occurred when the ratio a/b was equal to 1.1. However, their
cavity from the undisturbed temperature on the heated surface.
analysislikethatofMastersandSteinwasonlyconcernedwith
Since they were not in possession of either the computing
the deviation of the temperature in the axial cavity and did not
powerorthenumericalheatconductioncodesnowavailableto
address the error in measured heat flux.
the analyst, Masters and Stein performed a rigorous math-
4.3 Howey and DeCristina (3) were the first to perform an
ematical treatment of the deviation of the transient tempera-
actual thermal analysis of this measurement concept.Although
ture, T , on the bottom centerline of the cavity of radius, a, and
b
the explanation of modeling techniques is somewhat ambigu-
thickness, b, from the surface temperature T . The results of
s
ous in their paper, it is obvious that they used a finite element,
Masters and Stein indicated that the error in temperature
two dimensional axisymmetric model to produce temperature
measurement on the bottom centerline of the cavity would
profiles in a geometry simulating the null-point calorimeter.
decrease with increasing values of a/b and also decrease with
2 Temperature histories at time intervals down to 0.010 sec were
increasing values of the dimensionless time, at/b , where a is
obtained for a high heat-flux level on the surface of the
the thermal diffusity of the wall material. They also concluded
analytical model. Although the analytical results are not
that the most important factor in the error in temperature
presented in a format which would help the user/designer
measurementwastheratio a/bandtheerrorwasindependentof
optimize the sensor design, the authors did make significant
the level of heat flux. The conclusions of Masters and Stein
general conclusions about null point calorimeters. These in-
may appear to be somewhat elementary compared with our
clude: (1) “., thermocouple outputs can yield deceivingly fast
knowledge of the null-point concept today. However, the
response rates and erroneously high heating rates ( + 18 %)
identification and documentation of the measurement concept
when misused in inverse one-dimensional conduction solu-
was a major step in leading others to adapt this concept to the
tions.” (2) “The prime reason for holding the thermocouple
transient measurement of high heat fluxes in ground test
depth at R/E = 1.1 is to maximize thermocouple response at
facilities.
high heating rates for the minimum cavity depth.” (Note:
4.2 Beck and Hurwicz (2) expanded the analysis of Masters
R and E as used by Howey and DeChristina are the same terms
and Stein to include steady-state solutions and were the first to
label the method of measurement “the null-point concept.” as aand bwhicharedefinedin4.1andareusedthroughoutthis
document.) (3)Afinite length null-point calorimeter body may
They effectively used a digital computer to generate relatively
large quantities of analytical data from numerical methods. be considered semi-infinite for:
NOTE 1—1-T (0,t) = Surface temperature (x = 0) of a solid, semi-infinite slab at some time, t.
s
NOTE 2—2-T (0,b,t) = Temperature at r = 0, x = b of a slab with a cylindrical cavity at some time, t, heat flux, q, the same in both cases.
b
FIG. 1 Semi-infinite Slab with Cylindrical Cavity
E 598
~at! individually. Some of the conclusions reached were rather
# 0.3
L elementary and were previously reported in Refs (1-3). Others
were somewhat arbitrary and were stated without substantiat-
ing data. One specific conclusion concerns the ratio of the
4.4 Powers, Kennedy, and Rindal (4 and 5) were the first to
null-point cavity radius, a, to the cavity thickness, b. While
document using null point calorimeters in the swept mode.
stating that the optimum condition occurred when a = b, the
This method which is now used in almost all arc facilities has
authors of Ref (4) further state that when a = 0.305 mm (0.012
the advantages of (1) measuring the radial distributions across
in.) and b = 0.127 mm (0.005 in.); a/b = 2.4, the calculated
the arc jet, and (2) preserving the probe/sensor structural
heat flux will be 20 % higher than the actual heat flux. In more
integrity for repeated measurements. This technique involves
recent documentation using more accurate and sophisticated
sweeping the probe/sensor through the arc-heated flow field at
heat conduction computer codes as well as an established
a rate slow enough to allow the sensor to make accurate
numerical inverse heat conduction equation (6), the error in
measurements, yet fast enough to prevent model ablation.
indicated heat flux is shown to be considerably higher than
4.4.1 Following the pattern of Howey and DiCristina, Pow-
20 % and is highly time dependent.
ers et. al. stressed the importance of performing thermal
analyses to “characterize the response of a typical real null 4.5 The latest and most comprehensive thermal analysis of
point calorimeter to individually assess a variety of potential the null-point calorimeter concept was performed by Kidd and
errors, .”. Powers et. al. complain that Howey & DiCristina documented in Refs (6 and 7). This analytical work was
“. report substantial errors in some cases, but present no accomplished by using a finite element axisymmetric heat
generalized results or design guide lines.” They state concern- conduction code (7). The finite element model simulating the
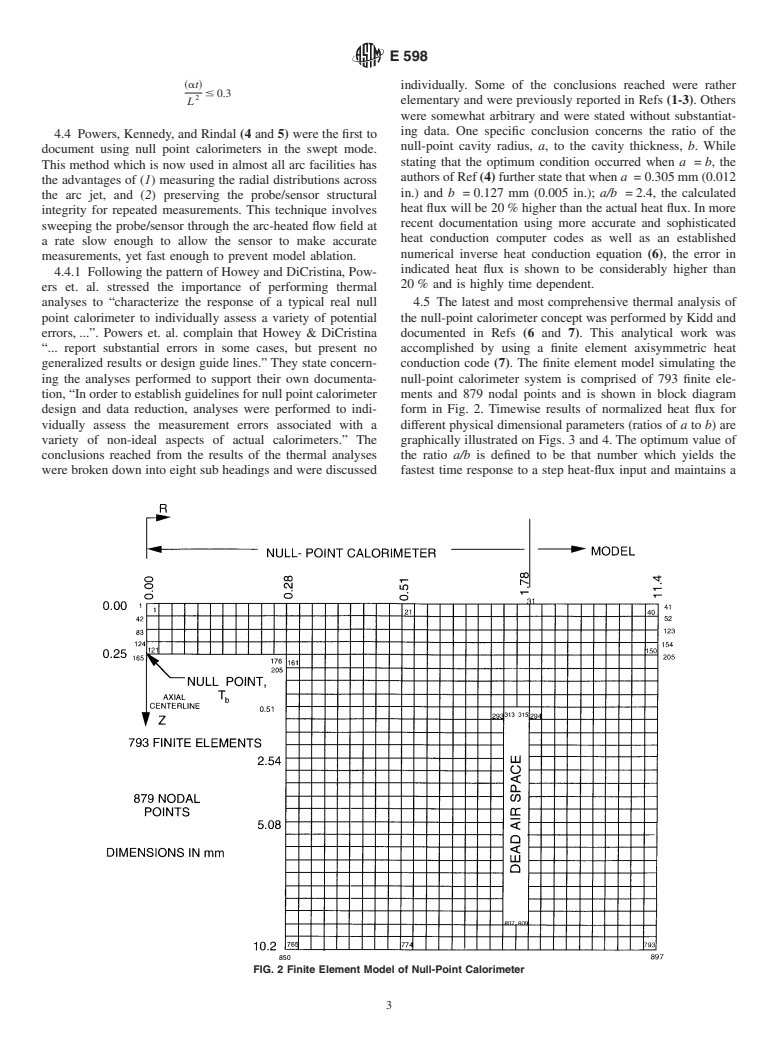
ing the analyses performed to support their own documenta- null-point calorimeter system is comprised of 793 finite ele-
tion, “In order to establish guidelines for null point calorimeter ments and 879 nodal points and is shown in block diagram
design and data reduction, analyses were performed to indi- form in Fig. 2. Timewise results of normalized heat flux for
vidually assess the measurement errors associated with a different physical dimensional parameters (ratios of a to b) are
variety of non-ideal aspects of actual calorimeters.” The graphically illustrated on Figs. 3 and 4. The optimum value of
conclusions reached from the results of the thermal analyses the ratio a/b is defined to be that number which yields the
were broken down into eight sub headings and were discussed fastest time response to a step heat-flux input and maintains a
FIG. 2 Finite Element Model of Null-Point Calorimeter
E 598
FIG. 3 Null-Point Calorimeter Analytical Time Response Data
FIG. 4 Null-Point Calorimeter Analytical Time Response Data
constant value of indicated q˙/input q˙ after the initial time flux—especially as the ratio of a/b is raised consistently above
response period. From Figs. 3 and 4, it can be seen that this 1.5. All of the users of null-point calorimeters assume that the
optimum value is about 1.4 for two families of curves for device simulates a semi-infinite body in the time period of
which the cavity radius, a, is held constant while the cavity interest. Therefore, the sensor is subject to the finite body
1/2
thickness, b,isvariedtospanawiderangeoftheratio a/b.This length, L, defined by L/(at) # 1.8 in order that the error in
is a slightly higher value than reported by earlier analysts. It is indicated heat flux does not exceed one percent (6 and 7). This
important to note that the analytical results do not necessarily restriction agrees well with the earlier work of Howey and
have to give a value of indicated q˙/input q˙ = 1.0 since this DiCristina (3).
difference can be calibrated in the laboratory. The data graphi- 4.6 Asection view sketch of a typical null-point calorimeter
cally illustrated on Figs. 3 and 4 and substantiate conclusions showing all important components and the physical configu-
drawn by the authors of Refs (3 nd 4) that the calculated heat ration of the sensor is shown in Fig. 5. The outside diameter is
flux can be considerably higher than the actual input heat 2.36 mm (0.093 in.), the length is 10.2 mm (0.40 in.), and the
E 598
FIG. 5 Section View Sketch of Null-Point Calorimeter
body material is oxygen-free high conductivity (OFHC) cop- foreign materials. Note that the null-point body has a small
per. Temperature at the null point is measured by a 0.508 mm flange at the front and back which creates an effective dead air
(0.020 in.) diam American National Standards Association space along the length of the cylinder to enhance one-
(ANSI) type K stainless steel-sheathed thermocouple with dimensional heat conduction and prevent radial conduction.
0.102 mm (0.004 in.) diam thermoelements. Although no For aerodynamic heat-transfer measurements, the null-point
thermocouple attachment is shown, it is assumed that the sensors are generally pressed into the stagnation position of a
individual thermocouple wires are in perfect contact with the sphere cone model of the same material (OFHC copper).
backsideofthecavityandpresentnoaddedthermalmasstothe 4.7 The value of the lumped thermal parameter of copper is
system. Details of installing thermocouples in the null point not a strong function of temperature. In fact, the value of
1/2
cavity and making a proper attachment of the thermocouple (rC k) for OFHC copper varies less than three percent from
p
with the copper slug are generally considered to be proprietary room temperature to the melting point, 1356 K (1981°F); (see
by the sensor manufacturers. Kidd in Ref (7) states that the Fig. 6). Thermal properties of OFHC copper are well docu-
attachment is made by thermal fusion without the addition of mented and data from different sources are in good agreement
1/2
FIG.6Variationof(rC k) with Temperature
p
E 598
(8). Most experimenters use the room temperature value of the tive results as would be experienced with other types of heat
parameter in processing data from
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.