ASTM E2022-99
(Practice)Standard Practice for Calculation of Weighting Factors for Tristimulus Integration
Standard Practice for Calculation of Weighting Factors for Tristimulus Integration
SCOPE
1.1 This practice describes the method to be used for calculating tables of weighting factors for tristimulus integration using custom spectral power distributions of illuminants or sources, or custom color-matching funtions.
1.2 This practice provides methods for calculating tables of values for use with spectral reflectance or transmittance data, which are corrected for the influences of finite bandpass. In addition, this practice provides methods for calculating weighting factors from spectral data which has not been bandpass corrected. In the latter case, a correction for the influence of bandpass on the resulting tristimulus values is built in to the tristimulus integration through the weighting factors.
1.3 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
Designation: E 2022 – 99
AMERICAN SOCIETY FOR TESTING AND MATERIALS
100 Barr Harbor Dr., West Conshohocken, PA 19428
Reprinted from the Annual Book of ASTM Standards. Copyright ASTM
Standard Practice for
Calculation of Weighting Factors for Tristimulus Integration
This standard is issued under the fixed designation E 2022; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
1. Scope tion. An illuminant is a table of agreed spectral power
distribution that may represent a source; thus, Illuminant A is a
1.1 This practice describes the method to be used for
standard spectral power distribution and Source A is the
calculating tables of weighting factors for tristimulus integra-
physical representation of that distribution. Illuminant D65 is a
tion using custom spectral power distributions of illuminants or
standard illuminant that represents average north sky daylight
sources, or custom color-matching functions.
but has no representative source.
1.2 This practice provides methods for calculating tables of
3.2.3 spectral power distribution, SPD, S(l),
values for use with spectral reflectance or transmittance data,
n—specification of an illuminant by the spectral composition
which are corrected for the influences of finite bandpass. In
of a radiometric quantity, such as radiance or radiant flux, as a
addition, this practice provides methods for calculating weight-
function of wavelength.
ing factors from spectral data which has not been bandpass
corrected. In the latter case, a correction for the influence of
4. Summary of Practice
bandpass on the resulting tristimulus values is built in to the
4.1 CIE color-matching functions are standardized at 1-nm
tristimulus integration through the weighting factors.
wavelength intervals. Tristimulus integration by multiplication
1.3 This standard does not purport to address all of the
of abridged spectral data into sets of weighting factors occurs
safety concerns, if any, associated with its use. It is the
at larger intervals, typically 10-nm or 20-nm; therefore, inter-
responsibility of the user of this standard to establish appro-
mediate 1-nm interval spectral data are missing, but needed.
priate safety and health practices and determine the applica-
4.2 Lagrange interpolating coefficients are calculated for the
bility of regulatory limitations prior to its use.
missing wavelengths. The Lagrange coefficients, when multi-
2. Referenced Documents plied into the appropriate measured spectral data, interpolate
the abridged spectrum to 1-nm interval. The 1-nm interval
2.1 ASTM Standards:
spectrum is then multiplied into the CIE 1-nm color-matching
E 284 Terminology of Appearance
data, and into the source spectral power distribution. Each
E 308 Practice for Computing the Colors of Objects by
separate term of this multiplication is collected into a value
Using the CIE System
associated with a measured spectral wavelength, thus forming
2.2 CIE Standard:
weighting factors for tristimulus integration.
CIE Standard S 002 Colorimetric Observers
4.3 A correction may be applied to the resulting table of
3. Terminology weighting factors to incorporate a correction for the spectral
data’s bandpass dependence.
3.1 Definitions—Appearance terms in this practice are in
accordance with Terminology E 284.
5. Significance and Use
3.2 Definitions of Terms Specific to This Standard:
5.1 This practice is intended to provide a method that will
3.2.1 illuminant, n—real or ideal radiant flux, specified by
yield uniformity of calculations used in making, matching, or
its spectral distribution over the wavelengths that, in illuminat-
controlling colors of objects. This uniformity is accomplished
ing objects, can affect their perceived colors.
by providing a method for calculation of weighting factors for
3.2.2 source, n—an object that produces light or other
tristimulus integration consistent with the methods utilized to
radiant flux, or the spectral power distribution of that light.
obtain the weighting factors for common illuminant-observer
3.2.2.1 Discussion—A source is an emitter of visible radia-
combinations contained in Practice E 308.
5.2 This practice should be utilized by persons desiring to
This practice is under the jurisdiction of ASTM Committee E-12 on Color and
calculate a set of weighting factors for tristimulus integration
Appearance and is the direct responsibility of Subcommittee D12.04 on Color and
who have custom source, or illuminant spectral power distri-
Appearance Analysis.
butions, or custom observer response functions.
Current edition approved June 10, 1999. Published August 1999.
5.3 This practice assumes that the measurement interval is
Annual Book of ASTM Standards, Vol 06.01.
Available from USNC-CIE Publications Office, TLA Lighting Consultants, 7
Pond Street, Salem, MA 01970.
E 2022
equal to the spectral bandwidth integral when applying correc- ~r!~r –2!~r –3!
L 5 (3)
tion for bandwidth.
~r –1!~r!~r –3!
L 5 (4)
6. Procedure 2
–2
6.1 Calculation of Lagrange Coeffıcients—Obtain by calcu-
~r –1!~r –2!~r!
L 5 (5)
lation, or by table look-up, a set of Lagrange interpolating
coefficients for each of the missing wavelengths.
for the cubic case, and to
6.1.1 The coefficients should be quadratic (three-point) in
r –1! r –2!
~ ~
the first and last missing interval, and cubic (four-point) in all
L 5 (6)
intervals between the first and the last missing interval.
6.1.2 Generalized Lagrange Coeffıcients—Lagrange coeffi- r r –2
~ !~ !
L 5 (7)
–1
cients may be calculated for any interval and number of
missing wavelengths by Eq 1:
~r –1!~r!
L 5 (8)
n 2
~r – r !
i
L ~r! 5 , for j 5 0,1,.n (1)
j )
~r – r !
i50 i�j
j i for the quadratic case. In each of the above equations, as
many or as few values of r as required are chosen to generate
where:
the necessary coefficients.
n 5 degree of coefficients being
6.1.3.1 Eq 2-8 are applicable when the spectral data are
calculated,
abridged at 10-nm or 20-nm intervals, and the interpolated
i and j 5 indices denoting the location
interval is regular with respect to the measurement interval,
along the abscissa,
presumably 1-nm.
p5 repetitive multiplication of
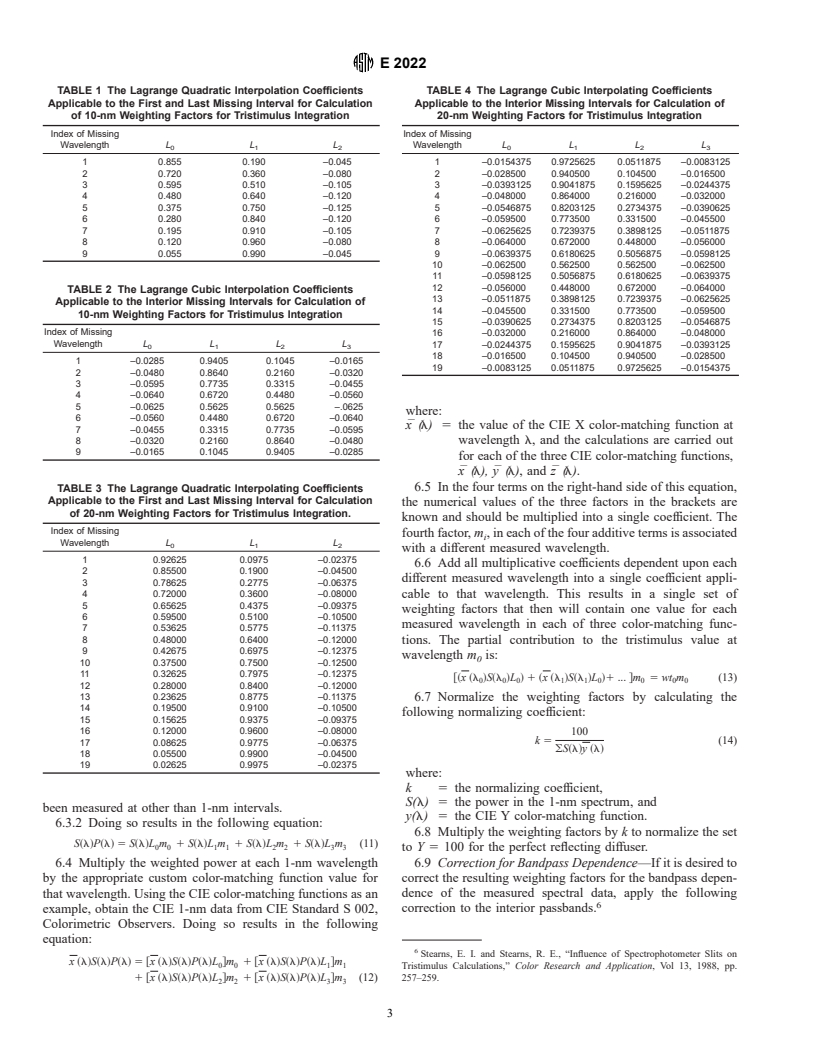
6.1.4 Tables 1-4 provide both quadratic and cubic Lagrange
the terms in the numerator
coefficients for 10-nm and 20-nm intervals.
and the denominator, and
indices of 5 chosen on the same scale as 6.2 With the Lagrange coefficients provided, the intermedi-
the interpolant, r the values i and j. ate missing spectral data may be predicted as follows:
6.1.2.1 Fig. 1 assist the user in selecting the values of i, j,
n
P~l! 5 L m (9)
and r for these calculations. (
i i
i50
6.1.2.2 Eq 1 is general and is applicable to any measurement
interval or interpolation interval, regular or irregular. where:
P 5 the value being interpolated at interval l,
6.1.3 10 and 20-nm Lagrange Coeffıcients—Where the
L 5 the Lagrange coefficients, and
measured spectral data have a regular or constant interval, the
m 5 the measured abridged spectral values.
equation reduces to the following:
Because the measured spectral values are as yet unknown, it
~r –1!~r –2!~r –3!
L 5 (2)
may be best to consider this equation in its expanded form:
–6
P~l! 5 L m 1 L m 1 L m 1 L m (10)
0 0 1 1 2 2 3 3
6.3 Multiply each P(l) by the 1-nm interval relative spectral
power of the source or illuminant being considered.
Hildebrand, F. B., Introduction to Numerical Analysis, Second Edition, Dover,
New York, 1974, Chapter 3.
6.3.1 It may be necessary to interpolate missing values of
Fairman, H. S., “The Calculation of Weight Factors for Tristimulus Integra-
the source spectral power distribution S(l), if the source has
tion.” Color Research and Application, Vol 10, 1985, pp. 199–203.
NOTE 1—The Values of i in Eq 1 are plotted above the abscissa and the values of r are plotted below for A) the first measurement interval; B) the
intermediate measurement intervals; and, C) the last measurement interval being interpolated.
FIG. 1
E 2022
TABLE 1 The Lagrange Quadratic Interpolation Coefficients TABLE 4 The Lagrange Cubic Interpolating Coefficients
Applicable to the First and Last Missing Interval for Calculation Applicable to the Interior Missing Intervals for Calculation of
of 10-nm Weighting Factors for Tristimulus Integration 20-nm Weighting Factors for Tristimulus Integration
Index of Missing Index of Missing
Wavelength L L L Wavelength L L L L
0 1 2 0 1 2 3
1 0.855 0.190 –0.045 1 –0.0154375 0.9725625 0.0511875 –0.0083125
2 0.720 0.360 –0.080 2 –0.028500 0.940500 0.104500 –0.016500
3 0.595 0.510 –0.105 3 –0.0393125 0.9041875 0.1595625 –0.0244375
4 0.480 0.640 –0.120 4 –0.048000 0.864000 0.216000 –0.032000
5 0.375 0.750 –0.125 5 –0.0546875 0.8203125 0.2734375 –0.0390625
6 0.280 0.840 –0.120 6 –0.059500 0.773500 0.331500 –0.045500
7 0.195 0.910 –0.105 7 –0.0625625 0.7239375 0.3898125 –0.0511875
8 0.120 0.960 –0.080 8 –0.064000 0.672000 0.448000 –0.056000
9 0.055 0.990 –0.045 9 –0.0639375 0.6180625 0.5056875 –0.0598125
10 –0.062500 0.562500 0.562500 –0.062500
11 –0.0598125 0.5056875 0.6180625 –0.0639375
12 –0.056000 0.448000 0.672000 –0.064000
TABLE 2 The Lagrange Cubic Interpolation Coefficients
13 –0.0511875 0.3898125 0.7239375 –0.0625625
Applicable to the Interior Missing Intervals for Calculation of
14 –0.045500 0.331500 0.773500 –0.059500
10-nm Weighting Factors for Tristimulus Integration
15 –0.0390625 0.2734375 0.8203125 –0.0546875
Index of Missing
16 –0.032000 0.216000 0.864000 –0.048000
Wavelength L L L L 17 –0.0244375 0.1595625 0.9041875 –0.0393125
0 1 2 3
18 –0.016500 0.104500 0.940500 –0.028500
1 –0.0285 0.9405 0.1045 –0.0165
19 –0.0083125 0.0511875 0.9725625 –0.0154375
2 –0.0480 0.8640 0.2160 –0.0320
3 –0.0595 0.7735 0.3315 –0.0455
4 –0.0640 0.6720 0.4480 –0.0560
5 –0.0625 0.5625 0.5625 –.0625
where:
6 –0.0560 0.4480 0.6720 –0.0640
x¯(l) 5 the value of the CIE X color-matching function at
7 –0.0455 0.3315 0.7735 –0.0595
8 –0.0320 0.2160 0.8640 –0.0480 wavelength l, and the calculations are carried out
9 –0.0165 0.1045 0.9405 –0.0285
for each of the three CIE color-matching functions,
x¯(l), y¯(l), and z¯(l).
6.5 In the four terms on the right-hand side of this equation,
TABLE 3 The Lagrange Quadratic Interpolating Coefficients
Applicable to the First and Last Missing Interval for Calculation
the numerical values of the three factors in the brackets are
of 20-nm Weighting Factors for Tristimulus Integration.
known and should be multiplied into a single coefficient. The
Index of Missing
fourth factor, m , in each of the four additive terms is associated
i
Wavelength L L L
0 1 2
with a different measured wavelength.
1 0.92625 0.0975 –0.02375
6.6 Add all multiplicative coefficients dependent upon each
2 0.85500 0.1900 –0.04500
different measured wavelength into a single coefficient appli-
3 0.78625 0.2775 –0.06375
4 0.72000 0.3600 –0.08000
cable to that wavelength. This results in a single set of
5 0.65625 0.4375 –0.09375
weighting factors that then will contain one value for each
6 0.59500 0.5100 –0.10500
measured wavelength in each of three color-matching func-
7 0.53625 0.5775 –0.11375
8 0.48000 0.6400 –0.12000 tions. The partial contribution to the tristimulus value at
9 0.42675 0.6975 –0.12375
wavelength m is:
10 0.37500 0.7500 –0.12500
11 0.32625 0.7975 –0.12375
@~x ~l !S~l !L ! 1 ~x ~l !S~l !L !1 . #m 5 wt m (13)
0 0 0 1 1 0 0 0 0
12 0.28000 0.8400 –0.12000
13 0.23625 0.8775 –0.11375
6.7 Normalize the weighting factors by calculating the
14 0.19500 0.9100 –0.10500
following normalizing coefficient:
15 0.15625 0.9375 –0.09375
16 0.12000 0.9600 –0.08000
k 5 (14)
17 0.08625 0.9775 –0.06375
(S~l!y ~l!
18 0.05500 0.9900 –0.04500
19 0.02625 0.9975 –0.02375
where:
k 5 the normalizing coefficient,
S(l) 5 the power in the 1-nm spectrum, and
been measured at other than 1-nm intervals.
y(l) 5 the CIE Y color-matching function.
6.3.2 Doing so results in the following equation:
6.8 Multiply the weighting factors by k to normalize the set
S~l!P~l! 5 S~l!L m 1 S~l!L m 1 S~l!L m 1 S~l!L m (11)
0 0 1 1 2 2 3 3
to Y 5 100 for the perfect reflecting diffuser.
6.9 Correction for Bandpass Dependence—If it is desired to
6.4 Multiply the weighted power at each 1-nm wavelength
by the appropriate custom color-matching function value for correct the resulting weighting factors for the bandpass depen-
dence of the measured spectral data, apply the following
that wavelength. Using the CIE color-matching functions as an
example, obtain the CIE 1-nm data from CIE Standard S 002, correction to the interior passbands.
Colorimetric Observers. Doing so results in the following
equation:
Stearns, E. I. and Stearns, R. E., “Influence of Spectrophotometer Slits on
x l!S l!P l! 5 x l!S l!P l!L m 1 x l!S l!P l!L m
~ ~ ~ @ ~ ~ ~ # @ ~ ~ ~ #
0 0 1 1
Tristimulus Calculations,” Color Research and Application, Vol 13, 1988, pp.
1 @x ~l!S~l!P~l!L #m 1 @x ~l!S~l!P~l!L #m (12) 257–259.
2 2 3 3
E 2022
W ~i! 5 –0.083 · W ~i–1! 1 1.166 · W ~i! – 0.083 · W ~i 1 1! 7. Precision
c M M M
(15)
7.1 The precision of the practice is limited only by the
where
precision of the data provided for the source spectral power
W 5 the indexed weight,
distribution. The CIE color-matching functions are precise to
c 5 a corrected weight, and
six digits by definition. The Lagrange coefficients are precise to
m 5 a weight calculated without bandpass correction.
seven digits.
The index i varies from the second measured passband to the
next to last measured passband. The following correction
8. Keywords
applies to the first and last measured passband:
8.1 color-matching functions; illuminant; illuminant-
W ~i! 5 1.166 · W ~i! – 0.083· W ~i 6 1! (16)
c M M
observer weights; source; tristimulus weighting factors
where the symbols are the same as those of Eq 16 and the
index i and 6 refers to the first and last measured passbands,
respectively.
APPENDIX
(Nonmandatory Information)
X1. EXAMPLE OF THE CALCULATIONS
TABLE X1.1 Spectral Power Distribution of Typical 3-Band Fluorescent Lamp with Correlated Color Temperature of 3000 K (1-nm
measurement interval)
l SPD l SPD l SPD l SPD l SPD l SPD
360 0.004880 450 0.014870 540 0.162400 630 0.111200 720 0.004410 810 0.000000
361 0.004595 451 0.015040 541 0.277600 631 0.102900 721 0.003505 811 0.000000
362 0.004310 452 0.015210 542 0.392800 632 0.094620 722 0.002600 812 0.000000
363 0.020290 453 0.014980 543 0.353900 633 0.062350 723 0.002470 813 0.000000
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.