ASTM E2709-14
(Practice)Standard Practice for Demonstrating Capability to Comply with an Acceptance Procedure
Standard Practice for Demonstrating Capability to Comply with an Acceptance Procedure
SIGNIFICANCE AND USE
4.1 This practice considers inspection procedures that may involve multiple-stage sampling, where at each stage one can decide to accept or to continue sampling, and the decision to reject is deferred until the last stage.
4.1.1 At each stage there are one or more acceptance criteria on the test results; for example, limits on each individual test result, or limits on statistics based on the sample of test results, such as the average, standard deviation, or coefficient of variation (relative standard deviation).
4.2 The methodology in this practice defines an acceptance region for a set of test results from the sampled population such that, at a prescribed confidence level, the probability that a sample from the population will pass the acceptance procedure is greater than or equal to a prespecified lower bound.
4.2.1 Having test results fall in the acceptance region is not equivalent to passing the acceptance procedure, but provides assurance that a sample would pass the acceptance procedure with a specified probability.
4.2.2 This information can be used for process demonstration, validation of test methods, and qualification of instruments, processes, and materials.
4.2.3 This information can be used for lot release (acceptance), but the lower bound may be conservative in some cases.
4.2.4 If the results are to be applied to future test results from the same process, then it is assumed that the process is stable and predictable. If this is not the case then there can be no guarantee that the probability estimates would be valid predictions of future process performance.
4.3 This methodology was originally developed (1-4)3 for use in two specific quality characteristics of drug products in the pharmaceutical industry but will be applicable for acceptance procedures in all industries.
4.4 Mathematical derivations would be required that are specific to the individual criteria of each test.
SCOPE
1.1 This practice provides a general methodology for evaluating single-stage or multiple-stage acceptance procedures which involve a quality characteristic measured on a numerical scale. This methodology computes, at a prescribed confidence level, a lower bound on the probability of passing an acceptance procedure, using estimates of the parameters of the distribution of test results from a sampled population.
1.2 For a prescribed lower probability bound, the methodology can also generate an acceptance limit table, which defines a set of test method outcomes (for example, sample averages and standard deviations) that would pass the acceptance procedure at a prescribed confidence level.
1.3 This approach may be used for demonstrating compliance with in-process, validation, or lot-release specifications.
1.4 The system of units for this practice is not specified.
1.5 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Buy Standard
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E2709 − 14 AnAmerican National Standard
Standard Practice for
Demonstrating Capability to Comply with an Acceptance
Procedure
This standard is issued under the fixed designation E2709; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope 3.1.1 characteristic, n—a property of items in a sample or
population which, when measured, counted or otherwise
1.1 This practice provides a general methodology for evalu-
observed, helps to distinguish between the items. E2282
ating single-stage or multiple-stage acceptance procedures
3.1.2 mean, n—of a population, µ, average or expected
which involve a quality characteristic measured on a numerical
¯
scale. This methodology computes, at a prescribed confidence value of a characteristic in a population, of a sample X , sum of
level, a lower bound on the probability of passing an accep- the observed values in a sample divided by the sample size.
tance procedure, using estimates of the parameters of the E2586
distribution of test results from a sampled population.
3.1.3 multiple-stage acceptance procedure, n—a procedure
that involves more than one stage of sampling and testing a
1.2 For a prescribed lower probability bound, the method-
givenqualitycharacteristicandoneormoreacceptancecriteria
ology can also generate an acceptance limit table, which
per stage.
defines a set of test method outcomes (for example, sample
averages and standard deviations) that would pass the accep-
3.1.4 standard deviation, n—of a population, σ, the square
tance procedure at a prescribed confidence level.
root of the average or expected value of the squared deviation
of a variable from its mean – of a sample, s, the square root of
1.3 This approach may be used for demonstrating compli-
the sum of the squared deviations of the observed values in the
ance with in-process, validation, or lot-release specifications.
sample divided by the sample size minus 1. E2586
1.4 The system of units for this practice is not specified.
3.1.5 test method, n—a definitive procedure that produces a
1.5 This standard does not purport to address all of the
test result. E2282
safety concerns, if any, associated with its use. It is the
3.2 Definitions of Terms Specific to This Standard:
responsibility of the user of this standard to establish appro-
3.2.1 acceptable parameter region, n—the set of values of
priate safety and health practices and determine the applica-
parameters characterizing the distribution of test results for
bility of regulatory limitations prior to use.
which the probability of passing the acceptance procedure is
greater than a prescribed lower bound.
2. Referenced Documents
3.2.2 acceptance region, n—the set of values of parameter
2.1 ASTM Standards:
estimates that will attain a prescribed lower bound on the
E456 Terminology Relating to Quality and Statistics
probability of passing an acceptance procedure at a prescribed
E2282 Guide for Defining the Test Result of a Test Method
level of confidence.
E2586 Practice for Calculating and Using Basic Statistics
3.2.3 acceptance limit, n—the boundary of the acceptance
3. Terminology
region, for example, the maximum sample standard deviation
test results for a given sample mean.
3.1 Definitions—See Terminology E456 for a more exten-
sive listing of terms in ASTM Committee E11 standards.
4. Significance and Use
4.1 This practice considers inspection procedures that may
This practice is under the jurisdiction ofASTM Committee E11 on Quality and
involve multiple-stage sampling, where at each stage one can
Statistics and is the direct responsibility of Subcommittee E11.20 on Test Method
decide to accept or to continue sampling, and the decision to
Evaluation and Quality Control.
reject is deferred until the last stage.
Current edition approved Oct. 1, 2014. Published October 2014. Originally
4.1.1 Ateachstagethereareoneormoreacceptancecriteria
approved in 2009. Last previous edition approved in 2012 as E2709 – 12. DOI:
10.1520/E2709-14.
on the test results; for example, limits on each individual test
For referenced ASTM standards, visit the ASTM website, www.astm.org, or
result, or limits on statistics based on the sample of test results,
contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
such as the average, standard deviation, or coefficient of
Standards volume information, refer to the standard’s Document Summary page on
the ASTM website. variation (relative standard deviation).
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
E2709 − 14
4.2 The methodology in this practice defines an acceptance P pass k 2 stage procedure $ max P S , P S , … , P S (2)
~ ! $ ~ ! ~ ! ~ !%
1 2 k
regionforasetoftestresultsfromthesampledpopulationsuch
5.3 Determine the contour of the region of parameter values
that, at a prescribed confidence level, the probability that a
for which the expression for the probability of passing the
sample from the population will pass the acceptance procedure
given acceptance procedure is at least equal to the required
is greater than or equal to a prespecified lower bound.
lower bound (LB) on the probability of acceptance (p). This
4.2.1 Having test results fall in the acceptance region is not
defines the acceptable parameter region.
equivalent to passing the acceptance procedure, but provides
5.4 For each value of a statistic or set of statistics, derive a
assurance that a sample would pass the acceptance procedure
joint confidence region for the distribution parameters at
with a specified probability.
confidence level, expressed as a percentage, of 100(1-α). The
4.2.2 This information can be used for process
size of sample to be taken, n, and the statistics to be used, must
demonstration, validation of test methods, and qualification of
be predetermined (see 5.6).
instruments, processes, and materials.
4.2.3 This information can be used for lot release
5.5 Determine the contour of the acceptance region, which
(acceptance),butthelowerboundmaybeconservativeinsome
consists of values of the statistics for which the confidence
cases.
region at level 100(1-α) is entirely contained in the acceptable
4.2.4 If the results are to be applied to future test results
parameter region. The acceptance limits lie on the contour of
from the same process, then it is assumed that the process is
the acceptance region.
stable and predictable. If this is not the case then there can be
5.6 To select the size of sample, n, to be taken, the
no guarantee that the probability estimates would be valid
probability that sample statistics will lie within acceptance
predictions of future process performance.
limits should be evaluated over a range of values of n, for
4.3 This methodology was originally developed (1-4) for
values of population parameters of practical interest, and for
use in two specific quality characteristics of drug products in
which probabilities of passing the given acceptance procedure
the pharmaceutical industry but will be applicable for accep-
are well above the lower bound. The larger the sample size n
tance procedures in all industries.
that is chosen, the larger will be the acceptance region and the
tighter the distribution of the statistics. Choose n so that the
4.4 Mathematical derivations would be required that are
probability of passing acceptance limits is greater than a
specific to the individual criteria of each test.
predetermined value.
5. Methodology
5.7 To use the acceptance limit, sample randomly from the
5.1 The process for defining the acceptance limits, starting
population. Compute statistics for the sample. If statistics fall
from the definition of the acceptance procedure, is outlined in
within the acceptance limits, then there is 1-α confidence that
this section. A computer program is normally required to
the probability of acceptance is at least p.
produce the acceptable parameter region and the acceptance
limits.
6. Procedures for Sampling from a Normal Distribution
5.1.1 An expression for the exact probability of passing the
6.1 An important class of procedures is for the case where
acceptance procedure might be intractable when the procedure
the quality characteristic is normally distributed. Particular
consists of multiple stages with multiple criteria, hence a lower
instructions for that case are given in this section, for two
bound for the probability may be used.
sampling methods, simple random and two-stage. In this
5.2 Express the probability of passing the acceptance pro-
standard these sampling methods are denoted Sampling Plan 1
cedure as a function of the parameters characterizing the
and Sampling Plan 2, respectively.
distribution of the quality characteristic for items in the
6.2 When the characteristic is normally distributed, param-
sampled population.
eters are the mean (µ) and standard deviation (σ)ofthe
5.2.1 For each stage in the procedure having multiple
population. The acceptable parameter region will be the region
acceptance criteria, determine the lower bound on the prob-
under a curve in the half-plane where µ is on the horizontal
ability of that stage as a function of the probabilities of passing
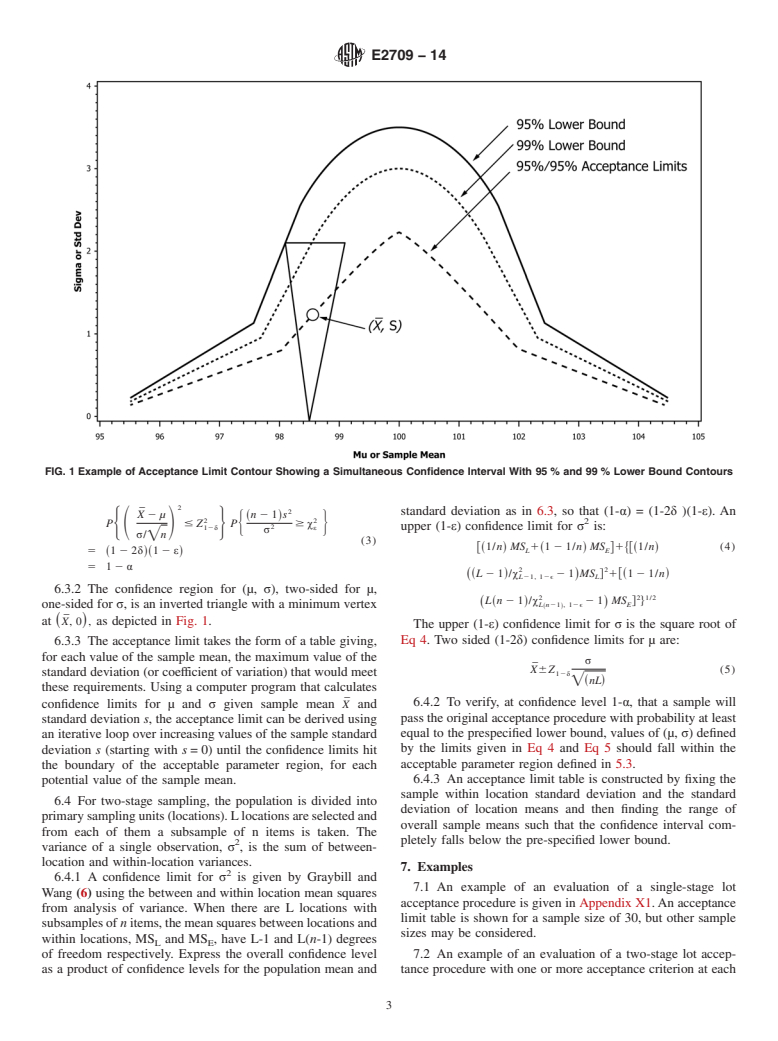
axis, σ on the vertical axis, such as that depicted in Fig. 1.
each of the criteria in the stage:
6.3 For simple random sampling from a normal population,
m
P~S ! 5 P~C and C … and C !$ 1 2 ~1 2 P~C !! (1)
i i1 i2 im (j51 ij
the method of Lindgren (5) constructs a simultaneous confi-
¯
where: dence region of (µ, σ) values from the sample average X and
the sample standard deviation s of n test results.
P(S) = is the probability of passing stage i,
i
P(C ) = is the probability of passing the j-th criterion of m
ij
6.3.1 Let Z and χ denote percentiles of the standard
p p
within the i-th stage.
normal distribution and of the chi-square distribution with n-1
5.2.2 Determine the lower bound on the probability of degrees of freedom, respectively. Given a confidence level
(1-α), choose δ and ε such that (1-α) = (1-2δ )(1-ε). Although
passing a k-stage procedure as a function of probabilities of
passing each of the individual stages: there are many choices for δ and ε that would satisfy this
= ~
equation, a reasonable choice is: ε512 12α and δ5 1
3 = !
2 12α /2 which equally splits the overall alpha between
The boldface numbers in parentheses refer to a list of references at the end of
this standard. estimating µ and σ. Then:
E2709 − 14
FIG. 1 Example of Acceptance Limit Contour Showing a Simultaneous Confidence Interval With 95 % and 99 % Lower Bound Contours
¯ standard deviation as in 6.3, so that (1-α) = (1-2δ )(1-ε). An
X 2 µ ~n 2 1!s
2 2
P # Z P $ χ
H J
12δ 2 ε upper (1-ε) confidence limit for σ is:
HS D J
σ
σ/=n
(3)
@~1/n! MS 1~1 21/n! MS #1$@~1/n! (4)
L E
5 ~1 2 2δ!~1 2 ε!
5 1 2 α
2 2
L 2 1 /χ 2 1 MS # 1 1 21/n
~ ! @~ !
~ !
L21, 12ϵ L
6.3.2 The confidence region for (µ, σ), two-sided for µ,
2 2 1/2
L n 2 1 /χ 2 1 MS # %
~ !
~ L n21,12ϵ ! E
one-sided for σ, is an inverted triangle with a minimum vertex ~ !
¯
~ !
at X,0 , as depicted in Fig. 1.
The upper (1-ε) confidence limit for σ is the square root of
Eq 4. Two sided (1-2δ) confidence limits for µ are:
6.3.3 The acceptance limit takes the form of a table giving,
for each value of the sample mean, the maximum value of the
σ
¯
X6Z (5)
standard deviation (or coefficient of variation) that would meet 12δ
=~nL!
these requirements. Using a computer program that calculates
¯
6.4.2 To verify, at confidence level 1-α, that a sample will
confidence limits for µ and σ given sample mean X and
pass the original acceptance procedure with probability at least
standard deviation s, the acceptance limit can be derived using
equal to the prespecified lower bound, values of (µ, σ) defined
an iterative loop over increasing values of the sample standard
by the limits given in Eq 4 and Eq 5 should fall within the
deviation s (starting with s = 0) until the confidence limits hit
acceptable parameter region defined in 5.3.
the boundary of the acceptable parameter region, for each
6.4.3 An acceptance limit table is constructed by fixing the
potential value of the sample mean.
sample within location standard deviation and the standard
6.4 For two-stage sampling, the population is divided into
deviation of location means and then finding the range of
primarysamplingunits(locations).Llocationsareselectedand
overall sample means such that the confidence interval com-
from each of them a subsample of n items is taken. The
pletely falls below the pre-specified lower bound.
variance of a single observation, σ , is the sum of between-
location and within-location variances.
7. Examples
6.4.1 A confidence limit for σ is given by Graybill and
7.1 An example of an evaluation of a single-stage lot
Wang (6) using the between and within location mean squares
acceptance procedure is given in Appendix X1.An acceptance
from analysis of variance. When there are L locations with
limit table is shown for a sample size of 30, but other sample
subsamplesof nitems,themeansquaresbetweenlocationsand
sizes may be considered.
within locations, MS and MS , have L-1 and L(n-1) degrees
L E
of freedom respectively. Express the overall confidence level 7.2 An example of an evaluation of a two-stage lot accep-
as a product of confidence levels for the population mean and tance procedure with one or more acceptance criterion at each
E2709 − 14
stage is given in Appendix X2. An acceptance limit table is 8. Keywords
shown for a sample size of 30.
8.1 acceptance limits; joint confidence regions; multiple-
7.3 An example of an evaluation of a two-stage lot accep-
stage acceptance procedures; specifications
tance procedure with one or more acceptance criteria at each
stage using Sampling Plan 2 is given in Appendix X3.An
acceptance limit table is shown for a sample size of 4 taken at
each of 15 locations for a total of 60 units tested.
APPENDIXES
(Nonmandatory Information)
X1. EXAMPLE: EVALUATION OF A SINGLE STAGE ACCEPTANCE PROCEDURE
X1.1 A single-stage lot acceptance procedure is stated as X1.5 The acceptance limit table for this example was
follows: Sample five units at random from the lot and measure generated by a computer program and is listed in Table X1.1.
a numerical quality characteristic (X) of each unit. Criterion:
The table corresponds to a sample size of 30 using a 95 %
i
Pass if all 5 individual units are between 95 and 105;
confidence interval and a
...
This document is not an ASTM standard and is intended only to provide the user of an ASTM standard an indication of what changes have been made to the previous version. Because
it may not be technically possible to adequately depict all changes accurately, ASTM recommends that users consult prior editions as appropriate. In all cases only the current version
of the standard as published by ASTM is to be considered the official document.
Designation: E2709 − 12 E2709 − 14 An American National Standard
Standard Practice for
Demonstrating Capability to Comply with an Acceptance
Procedure
This standard is issued under the fixed designation E2709; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope
1.1 This practice provides a general methodology for evaluating single-stage or multiple-stage acceptance procedures which
involve a quality characteristic measured on a numerical scale. This methodology computes, at a prescribed confidence level, a
lower bound on the probability of passing an acceptance procedure, using estimates of the parameters of the distribution of test
results from a sampled population.
1.2 For a prescribed lower probability bound, the methodology can also generate an acceptance limit table, which defines a set
of test method outcomes (for example, sample averages and standard deviations) that would pass the acceptance procedure at a
prescribed confidence level.
1.3 This approach may be used for demonstrating compliance with in-process, validation, or lot-release specifications.
1.4 The system of units for this practice is not specified.
1.5 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility
of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory
limitations prior to use.
2. Referenced Documents
2.1 ASTM Standards:
E456 Terminology Relating to Quality and Statistics
E2282 Guide for Defining the Test Result of a Test Method
E2586 Practice for Calculating and Using Basic Statistics
3. Terminology
3.1 Definitions—See Terminology E456 for a more extensive listing of terms in ASTM Committee E11 standards.
3.1.1 characteristic, n—a property of items in a sample or population which, when measured, counted or otherwise observed,
helps to distinguish between the items. E2282
¯
3.1.2 mean, n—of a population, μ, average or expected value of a characteristic in a population, of a sampleX , sum of the
observed values in a sample divided by the sample size. E2586
3.1.3 multiple-stage acceptance procedure, n—a procedure that involves more than one stage of sampling and testing a given
quality characteristic and one or more acceptance criteria per stage.
3.1.4 standard deviation, n—of a population, σ, the square root of the average or expected value of the squared deviation of a
variable from its mean – of a sample, s, the square root of the sum of the squared deviations of the observed values in the sample
divided by the sample size minus 1. E2586
3.1.5 test method, n—a definitive procedure that produces a test result. E2282
3.2 Definitions of Terms Specific to This Standard:
This practice is under the jurisdiction of ASTM Committee E11 on Quality and Statistics and is the direct responsibility of Subcommittee E11.20 on Test Method
Evaluation and Quality Control.
Current edition approved Nov. 1, 2012Oct. 1, 2014. Published December 2012October 2014. Originally approved in 2009. Last previous edition approved in 20112012
as E2709 – 11.E2709 – 12. DOI: 10.1520/E2709-12.10.1520/E2709-14.
For referenced ASTM standards, visit the ASTM website, www.astm.org, or contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM Standards
volume information, refer to the standard’s Document Summary page on the ASTM website.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
E2709 − 14
3.2.1 acceptable parameter region, n—the set of values of parameters characterizing the distribution of test results for which
the probability of passing the acceptance procedure is greater than a prescribed lower bound.
3.2.2 acceptance region, n—the set of values of parameter estimates that will attain a prescribed lower bound on the probability
of passing an acceptance procedure at a prescribed level of confidence.
3.2.3 acceptance limit, n—the boundary of the acceptance region, for example, the maximum sample standard deviation test
results for a given sample mean.
4. Significance and Use
4.1 This practice considers inspection procedures that may involve multiple-stage sampling, where at each stage one can decide
to accept or to continue sampling, and the decision to reject is deferred until the last stage.
4.1.1 At each stage there are one or more acceptance criteria on the test results; for example, limits on each individual test result,
or limits on statistics based on the sample of test results, such as the average, standard deviation, or coefficient of variation (relative
standard deviation).
4.2 The methodology in this practice defines an acceptance region for a set of test results from the sampled population such that,
at a prescribed confidence level, the probability that a sample from the population will pass the acceptance procedure is greater
than or equal to a prespecified lower bound.
4.2.1 Having test results fall in the acceptance region is not equivalent to passing the acceptance procedure, but provides
assurance that a sample would pass the acceptance procedure with a specified probability.
4.2.2 This information can be used for process demonstration, validation of test methods, and qualification of instruments,
processes, and materials.
4.2.3 This information can be used for lot release (acceptance), but the lower bound may be conservative in some cases.
4.2.4 If the results are to be applied to future test results from the same process, then it is assumed that the process is stable
and predictable. If this is not the case then there can be no guarantee that the probability estimates would be valid predictions of
future process performance.
4.3 This methodology was originally developed (1-4) for use in two specific quality characteristics of drug products in the
pharmaceutical industry but will be applicable for acceptance procedures in all industries.
4.4 Mathematical derivations would be required that are specific to the individual criteria of each test.
5. Methodology
5.1 The process for defining the acceptance limits, starting from the definition of the acceptance procedure, is outlined in this
section. A computer program is normally required to produce the acceptable parameter region and the acceptance limits.
5.1.1 An expression for the exact probability of passing the acceptance procedure might be intractable when the procedure
consists of multiple stages with multiple criteria, hence a lower bound for the probability may be used.
5.2 Express the probability of passing the acceptance procedure as a function of the parameters characterizing the distribution
of the quality characteristic for items in the sampled population.
5.2.1 For each stage in the procedure having multiple acceptance criteria, determine the lower bound on the probability of that
stage as a function of the probabilities of passing each of the criteria in the stage:
m
P S 5 P C and C … and C $ 12 12 P C (1)
~ ! ~ ! ~ ~ !!
i i1 i2 im (j51 ij
where:
P(S ) = is the probability of passing stage i,
i
P(C ) = is the probability of passing the j-th criterion of m within the i-th stage.
ij
5.2.2 Determine the lower bound on the probability of passing a k-stage procedure as a function of probabilities of passing each
of the individual stages:
P ~pass k 2 stage procedure!$ max$P~S !, P~S !, … , P~S !% (2)
1 2 k
5.3 Determine the contour of the region of parameter values for which the expression for the probability of passing the given
acceptance procedure is at least equal to the required lower bound (LB) on the probability of acceptance (p). This defines the
acceptable parameter region.
5.4 For each value of a statistic or set of statistics, derive a joint confidence region for the distribution parameters at confidence
level, expressed as a percentage, of 100(1-α). The size of sample to be taken, n, and the statistics to be used, must be predetermined
(see 5.6).
The boldface numbers in parentheses refer to a list of references at the end of this standard.
E2709 − 14
5.5 Determine the contour of the acceptance region, which consists of values of the statistics for which the confidence region
at level 100(1-α) is entirely contained in the acceptable parameter region. The acceptance limits lie on the contour of the acceptance
region.
5.6 To select the size of sample, n, to be taken, the probability that sample statistics will lie within acceptance limits should be
evaluated over a range of values of n, for values of population parameters of practical interest, and for which probabilities of
passing the given acceptance procedure are well above the lower bound. The larger the sample size n that is chosen, the larger will
be the acceptance region and the tighter the distribution of the statistics. Choose n so that the probability of passing acceptance
limits is greater than a predetermined value.
5.7 To use the acceptance limit, sample randomly from the population. Compute statistics for the sample. If statistics fall within
the acceptance limits, then there is 1-α confidence that the probability of acceptance is at least p.
6. Procedures for Sampling from a Normal Distribution
6.1 An important class of procedures is for the case where the quality characteristic is normally distributed. Particular
instructions for that case are given in this section, for two sampling methods, simple random and two-stage. In this standard these
sampling methods are denoted Sampling Plan 1 and Sampling Plan 2, respectively.
6.2 When the characteristic is normally distributed, parameters are the mean (μ) and standard deviation (σ) of the population.
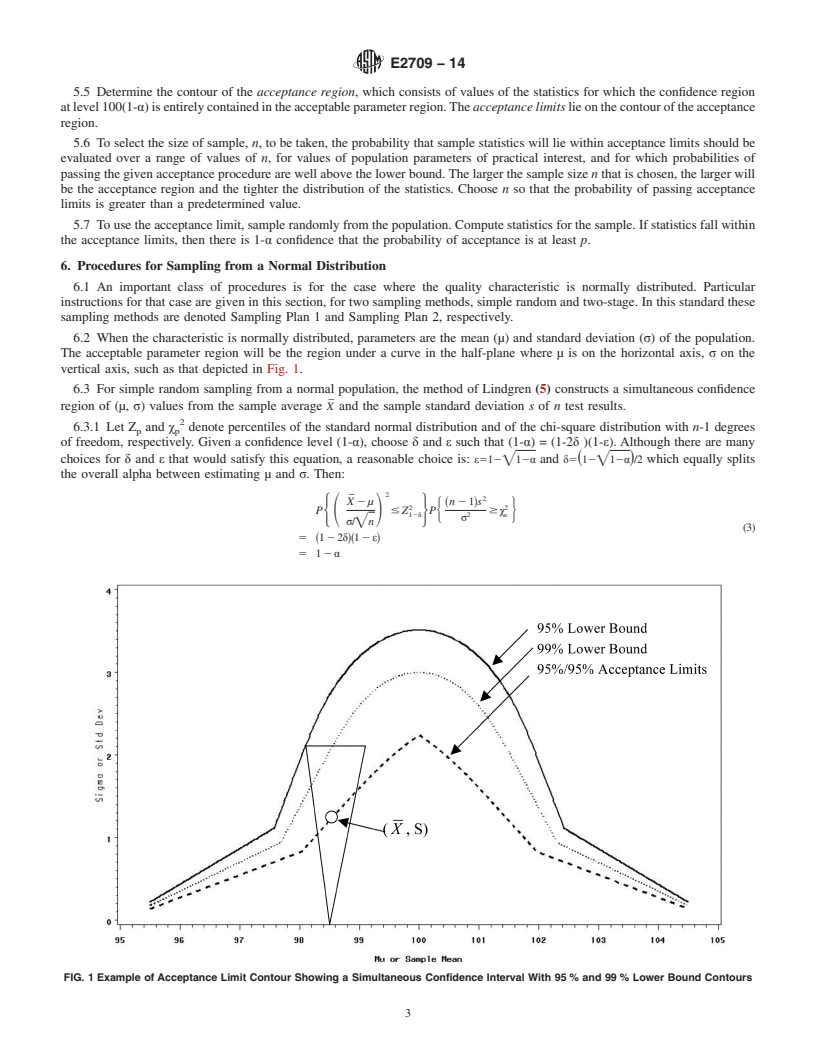
The acceptable parameter region will be the region under a curve in the half-plane where μ is on the horizontal axis, σ on the
vertical axis, such as that depicted in Fig. 1.
6.3 For simple random sampling from a normal population, the method of Lindgren (5) constructs a simultaneous confidence
¯
region of (μ, σ) values from the sample average X and the sample standard deviation s of n test results.
6.3.1 Let Z and χ denote percentiles of the standard normal distribution and of the chi-square distribution with n-1 degrees
p p
of freedom, respectively. Given a confidence level (1-α), choose δ and ε such that (1-α) = (1-2δ )(1-ε). Although there are many
choices for δ and ε that would satisfy this equation, a reasonable choice is: ε512=12α and δ5~12=12α!/2 which equally splits
the overall alpha between estimating μ and σ. Then:
¯
X 2 μ n 2 1 s
~ !
2 2
P # Z P $χ
H J
HS D 12δJ 2 ε
σ
σ/=n
(3)
5 12 2δ 12ε
~ !~ !
5 12α
FIG. 1 Example of Acceptance Limit Contour Showing a Simultaneous Confidence Interval With 95 % and 99 % Lower Bound Contours
E2709 − 14
¯
6.3.2 The confidence region for (μ, σ), two-sided for μ, one-sided for σ, is an inverted triangle with a minimum vertex at ~X, 0!,
as depicted in Fig. 1.
6.3.3 The acceptance limit takes the form of a table giving, for each value of the sample mean, the maximum value of the
standard deviation (or coefficient of variation) that would meet these requirements. Using a computer program that calculates
¯
confidence limits for μ and σ given sample mean X and standard deviation s, the acceptance limit can be derived using an iterative
loop over increasing values of the sample standard deviation s (starting with s = 0) until the confidence limits hit the boundary of
the acceptable parameter region, for each potential value of the sample mean.
6.4 For two-stage sampling, the population is divided into primary sampling units (locations). L locations are selected and from
each of them a subsample of n items is taken. The variance of a single observation, σ , is the sum of between-location and
within-location variances.
6.4.1 A confidence limit for σ is given by Graybill and Wang (6) using the between and within location mean squares from
analysis of variance. When there are L locations with subsamples of n items, the mean squares between locations and within
locations, MS and MS , have L-1 and L(n-1) degrees of freedom respectively. Express the overall confidence level as a product
L E
of confidence levels for the population mean and standard deviation as in 6.3, so that (1-α) = (1-2δ )(1-ε). An upper (1-ε) confidence
limit for σ is:
1/n MS 1 12 1/n MS 1 1/n (4)
@~ ! ~ ! # $@~ !
L E
2 2
L 2 1 /χ 2 1 MS # 1 12 1/n
~~ ! ! @~ !
L21, 12ϵ L
2 2 1/2
L~n 2 1!/χ 2 1 MS # %
~ !
L n21 , 12ϵ E
~ !
The upper (1-ε) confidence limit for σ is the square root of Eq 4. Two sided (1-2δ) confidence limits for μ are:
σ
¯
X6Z (5)
12δ
= nL
~ !
6.4.2 To verify, at confidence level 1-α, that a sample will pass the original acceptance procedure with probability at least equal
to the prespecified lower bound, values of (μ, σ) defined by the limits given in Eq 4 and Eq 5 should fall within the acceptable
parameter region defined in 5.3.
6.4.3 An acceptance limit table is constructed by fixing the sample within location standard deviation and the standard deviation
of location means and then finding the range of overall sample means such that the confidence interval completely falls below the
pre-specified lower bound.
7. Examples
7.1 An example of an evaluation of a single-stage lot acceptance procedure is given in Appendix X1. An acceptance limit table
is shown for a sample size of 30, but other sample sizes may be considered.
7.2 An example of an evaluation of a two-stage lot acceptance procedure with one or more acceptance criterion at each stage
is given in Appendix X2. An acceptance limit table is shown for a sample size of 30.
7.3 An example of an evaluation of a two-stage lot acceptance procedure with one or more acceptance criteria at each stage
using Sampling Plan 2 is given in Appendix X3. An acceptance limit table is shown for a sample size of 4 taken at each of 15
locations for a total of 60 units tested.
8. Keywords
8.1 acceptance limits; joint confidence regions; multiple-stage acceptance procedures; specifications
E2709 − 14
APPENDIXES
(Nonmandatory Information)
X1. EXAMPLE: EVALUATION OF A SINGLE STAGE ACCEPTANCE PROCEDURE
X1
...








Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.