iTeh StandardsiTeh Standards
EURUSD
Your shopping cart is empty.
ASTM

ASTM E637-05(2011)

(Test Method)

Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure

Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure

SIGNIFICANCE AND USE
The purpose of this test method is to provide a standard calculation of the stagnation enthalpy of an aerodynamic simulation device using the heat transfer theory and measured values of stagnation point heat transfer and pressure. A stagnation enthalpy obtained by this test method gives a consistent set of data, along with heat transfer and stagnation pressure for ablation computations.
SCOPE
1.1 This test method covers the calculation from heat transfer theory of the stagnation enthalpy from experimental measurements of the stagnation-point heat transfer and stagnation pressure.
1.2 Advantages:  
1.2.1 A value of stagnation enthalpy can be obtained at the location in the stream where the model is tested. This value gives a consistent set of data, along with heat transfer and stagnation pressure, for ablation computations.
1.2.2 This computation of stagnation enthalpy does not require the measurement of any arc heater parameters.
1.3 Limitations and Considerations—There are many factors that may contribute to an error using this type of approach to calculate stagnation enthalpy, including:
1.3.1 Turbulence—The turbulence generated by adding energy to the stream may cause deviation from the laminar equilibrium heat transfer theory.
1.3.2 Equilibrium, Nonequilibrium, or Frozen State of Gas—The reaction rates and expansions may be such that the gas is far from thermodynamic equilibrium.
1.3.3 Noncatalytic Effects—The surface recombination rates and the characteristics of the metallic calorimeter may give a heat transfer deviation from the equilibrium theory.
1.3.4 Free Electric Currents—The arc-heated gas stream may have free electric currents that will contribute to measured experimental heat transfer rates.
1.3.5 Nonuniform Pressure Profile—A nonuniform pressure profile in the region of the stream at the point of the heat transfer measurement could distort the stagnation point velocity gradient.
1.3.6 Mach Number Effects—The nondimensional stagnation-point velocity gradient is a function of the Mach number. In addition, the Mach number is a function of enthalpy and pressure such that an iterative process is necessary.
1.3.7 Model Shape—The nondimensional stagnation-point velocity gradient is a function of model shape.
1.3.8 Radiation Effects—The hot gas stream may contribute a radiative component to the heat transfer rate.
1.3.9 Heat Transfer Rate Measurement—An error may be made in the heat transfer measurement (see Method E469 and Test Methods E422, E457, E459, and E511).
1.3.10 Contamination—The electrode material may be of a large enough percentage of the mass flow rate to contribute to the heat transfer rate measurement.
1.4 The values stated in SI units are to be regarded as standard. No other units of measurement are included in this standard.
1.4.1 Exception—The values given in parentheses are for information only.
1.5 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.

General Information

Status
Historical
Publication Date
30-Sep-2011
ICS
17.200.10 - Heat. Calorimetry
Technical Committee
E21 - Space Simulation and Applications of Space Technology
Drafting Committee
E21.08 - Thermal Protection
Current Stage
Ref Project

Relations

Replaces
ASTM E637-05 - Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure
Effective Date
01-Oct-2011

Buy Standard

ASTM E637-05(2011) - Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and PressureASTM E637-05(2011) - Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure
PreviousNext
Standard
ASTM E637-05(2011) - Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure
English language
16 pages
sale 15% off
Preview
sale 15% off
Preview

Standards Content (Sample)


NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E637 − 05(Reapproved 2011)
Standard Test Method for
Calculation of Stagnation Enthalpy from Heat Transfer
Theory and Experimental Measurements of Stagnation-Point
Heat Transfer and Pressure
This standard is issued under the fixed designation E637; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
INTRODUCTION
The enthalpy (energy per unit mass) determination in a hot gas aerodynamic simulation device is
a difficult measurement. Even at temperatures that can be measured with thermocouples, there are
many corrections to be made at 600 K and above. Methods that are used for temperatures above the
range of thermocouples that give bulk or average enthalpy values are energy balance (see Practice
E341), sonic flow (1, 2), and the pressure rise method (3). Local enthalpy values (thus distribution)
may be obtained by using either an energy balance probe (see Method E470), or the spectrometric
technique described in Ref (4).
1. Scope 1.3.3 Noncatalytic Effects—Thesurfacerecombinationrates
and the characteristics of the metallic calorimeter may give a
1.1 This test method covers the calculation from heat
heat transfer deviation from the equilibrium theory.
transfer theory of the stagnation enthalpy from experimental
1.3.4 Free Electric Currents—The arc-heated gas stream
measurements of the stagnation-point heat transfer and stagna-
mayhavefreeelectriccurrentsthatwillcontributetomeasured
tion pressure.
experimental heat transfer rates.
1.2 Advantages:
1.3.5 Nonuniform Pressure Profile—Anonuniform pressure
1.2.1 Avalue of stagnation enthalpy can be obtained at the profile in the region of the stream at the point of the heat
location in the stream where the model is tested. This value transfer measurement could distort the stagnation point veloc-
gives a consistent set of data, along with heat transfer and ity gradient.
stagnation pressure, for ablation computations. 1.3.6 Mach Number Effects—The nondimensional
stagnation-point velocity gradient is a function of the Mach
1.2.2 This computation of stagnation enthalpy does not
number.Inaddition,theMachnumberisafunctionofenthalpy
require the measurement of any arc heater parameters.
and pressure such that an iterative process is necessary.
1.3 Limitations and Considerations—There are many fac-
1.3.7 Model Shape—The nondimensional stagnation-point
tors that may contribute to an error using this type of approach
velocity gradient is a function of model shape.
to calculate stagnation enthalpy, including:
1.3.8 Radiation Effects—The hot gas stream may contribute
1.3.1 Turbulence—The turbulence generated by adding en-
a radiative component to the heat transfer rate.
ergy to the stream may cause deviation from the laminar
1.3.9 Heat Transfer Rate Measurement—An error may be
equilibrium heat transfer theory.
made in the heat transfer measurement (see Method E469 and
1.3.2 Equilibrium, Nonequilibrium, or Frozen State of
Test Methods E422, E457, E459, and E511).
Gas—The reaction rates and expansions may be such that the
1.3.10 Contamination—The electrode material may be of a
gas is far from thermodynamic equilibrium.
large enough percentage of the mass flow rate to contribute to
the heat transfer rate measurement.
1.4 The values stated in SI units are to be regarded as
This test method is under the jurisdiction of ASTM Committee E21 on Space
standard. No other units of measurement are included in this
Simulation andApplications of SpaceTechnology and is the direct responsibility of
standard.
Subcommittee E21.08 on Thermal Protection.
1.4.1 Exception—The values given in parentheses are for
Current edition approved Oct. 1, 2011. Published April 2012. Originally
approved in 1978. Last previous edition approved in 2005 as E637–05. DOI:
information only.
10.1520/E0637-05R11.
1.5 This standard does not purport to address all of the
The boldface numbers in parentheses refer to the list of references appended to
this method. safety concerns, if any, associated with its use. It is the
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
E637 − 05 (2011)
TABLE 1 Heat Transfer and Enthalpy Computation Constants for
responsibility of the user of this standard to establish appro-
Various Gases
priate safety and health practices and determine the applica-
1/2 1/2 1/2 1/2
K , kg/(N ·m ·s) K ,(N ·m ·s)/kg
bility of regulatory limitations prior to use. i M
Gas
3/2 1/2 3/2 1/2
(lb/(ft ·s·atm )) ((ft ·s·atm )/lb)
−4
Air 3.905 × 10 (0.0461) 2561 (21.69)
2. Referenced Documents
−4
Argon 5.513 × 10 (0.0651) 1814 (15.36)
−4
2.1 ASTM Standards: Carbon dioxide 4.337 × 10 (0.0512) 2306 (19.53)
−4
Hydrogen 1.287 × 10 (0.0152) 7768 (65.78)
E341Practice for Measuring Plasma Arc Gas Enthalpy by
−4
Nitrogen 3.650 × 10 (0.0431) 2740 (23.20)
Energy Balance
E422Test Method for Measuring Heat Flux Using a Water-
Cooled Calorimeter
flow theory which becomes inaccurate for M <2. An im-
E457Test Method for Measuring Heat-Transfer Rate Using
oo
proved Mach number dependence at lower Mach numbers can
a Thermal Capacitance (Slug) Calorimeter
beobtainedbyremovingthe“modified”Newtonianexpression
E459Test Method for Measuring Heat Transfer Rate Using
andreplacingitwithamoreappropriateexpressionasfollows:
a Thin-Skin Calorimeter
E469Measuring Heat Flux Using a Multiple-Wafer Calo- 0.5
β D/U
~ !
K q˙ oo
Eq 3
M
rimeter (Withdrawn 1982) H 2 H 5 F G (2)
0.5
e w
P /R β D/U
~ !
~ !
t oo x50
E470Measuring Gas Enthalpy Using Calorimeter Probes
(Withdrawn 1982) Where the “modified” Newtonian stagnation-point velocity
E511TestMethodforMeasuringHeatFluxUsingaCopper- gradient is given by:
Constantan Circular Foil, Heat-Flux Transducer 2 0.5
4 γ 2 1 M 12
@~ ! #
oo
~β D/U ! 5 (3)
F G
oo 2
x50
γ M
oo
3. Significance and Use
A potential problem exists when using Eq 3 to remove the
3.1 The purpose of this test method is to provide a standard
“modified” Newtonian velocity gradient because of the singu-
calculation of the stagnation enthalpy of an aerodynamic
larity at M =0. The procedure recommended here should be
oo
simulation device using the heat transfer theory and measured
limited to M > 0.1
oo
values of stagnation point heat transfer and pressure. A
stagnation enthalpy obtained by this test method gives a
where:
consistent set of data, along with heat transfer and stagnation
−1
β = stagnation-point velocity gradient, s ,
pressure for ablation computations.
D = hemispherical diameter, m (or ft),
U = freestream velocity, m/s (or ft/s),
∞
4. Enthalpy Computations
(βD/U ) = dimensionless stagnation velocity gradient,
∞ x=0
4.1 This method of calculating the stagnation enthalpy is
K = enthalpy computation constant,
M
1/2 1/2 3/2 1/2
based on experimentally measured values of the stagnation-
(N ·m · s)/kg or (ft ·atm ·s)/lb, and
pointheattransferrateandpressuredistributionandtheoretical M∞ = the freestream Mach number.
calculation of laminar equilibrium catalytic stagnation-point
For subsonic Mach numbers, an expression for (βD/U )
∞ x=0
heat transfer on a hemispherical body. The equilibrium cata-
for a hemisphere is given in Ref (6) as follows:
lytic theoretical laminar stagnation-point heat transfer rate for
βD
a hemispherical body is as follows (5): 2
5 3 2 0.755 M M ,1 (4)
S D ~ !
x50 ` `
U
`
R
For a Mach number of 1 or greater, (βD/U ) for a
q 5 K ~H 2 H ! (1)
Œ
i e w ∞ x=0
P
t
hemisphere based on “classical” Newtonian flow theory is
presented in Ref (7) as follows:
where:
2 2
1 0.5
q = stagnation-pointheattransferrate,W/m (orBtu/ft ·s),
γ 2 1 γ21
P = model stagnation pressure, Pa (or atm), 11
t
8 γ 2 1 M 2 12 2
βD @~ ! #
`
R = hemispherical nose radius, m (or ft),
S D
x50
~γ 2 1!M 2 12
U ~γ11!M 2 @ #
`
` `
H = stagnation enthalpy, J/kg (or Btu/lb),
5 6
3 4
e
2γM 2 2 ~γ 2 1!
H = wall enthalpy, J/kg (or Btu/lb), and `
w
K = heat transfer computation constant.
(5)
i
4.2 Low Mach Number Correction—Eq 1 is simple and
Avariationof(βD/U ) with M andγisshowninFig.1.
∞ x=0 ∞
convenient to use since K can be considered approximately
i The value of the Newtonian dimensionless velocity gradient
constant(seeTable1).However,Eq1isbasedonastagnation-
approaches a constant value as the Mach number approaches
point velocity gradient derived using “modified” Newtonian
infinity:
βD γ 2 1
For referenced ASTM standards, visit the ASTM website, www.astm.org, or 5 4 (6)
S D ΠS D
x50,M→`
U γ
`
contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
Standards volume information, refer to the standard’s Document Summary page on
and thus, sinceγ, the ratio of specific heats, is a function of
the ASTM website.
enthalpy, (βD/U ) is also a function of enthalpy.Again, an
The last approved version of this historical standard is referenced on ∞ x=0
www.astm.org. iteration is necessary. From Fig. 1, it can be seen that
E637 − 05 (2011)
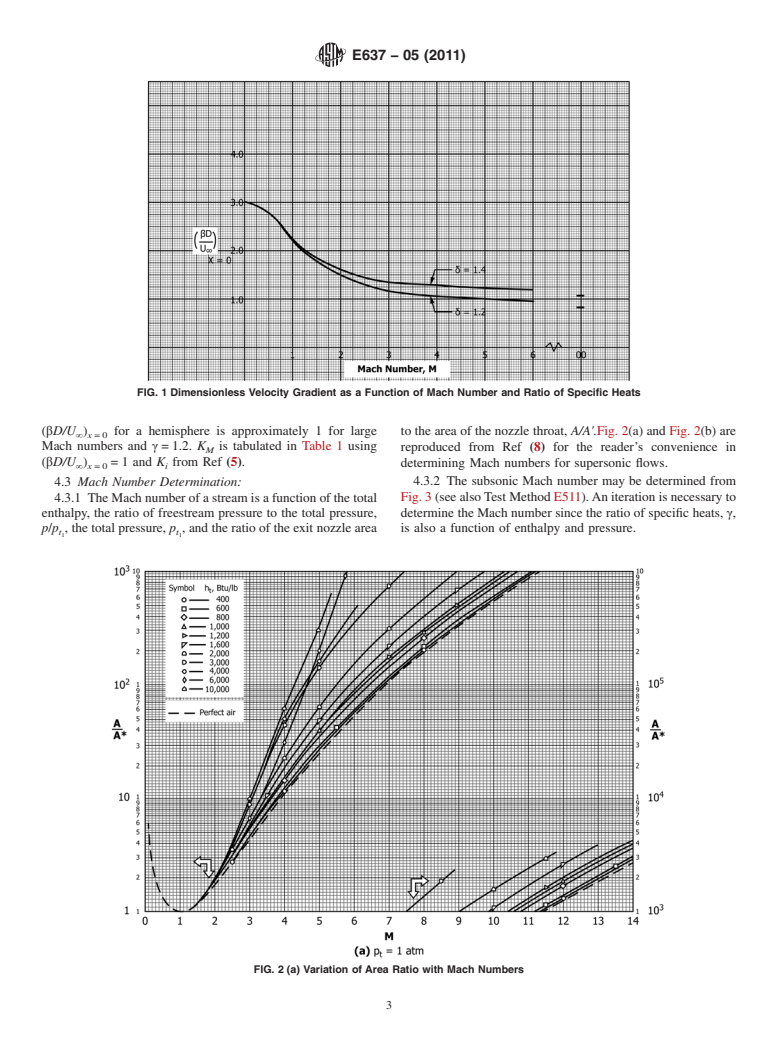
FIG. 1 Dimensionless Velocity Gradient as a Function of Mach Number and Ratio of Specific Heats
(βD/U ) for a hemisphere is approximately 1 for large to the area of the nozzle throat, A/A'.Fig. 2(a) and Fig. 2(b) are
∞ x=0
Mach numbers and γ=1.2. K is tabulated in Table 1 using reproduced from Ref (8) for the reader’s convenience in
M
(βD/U ) =1 and K from Ref (5).
determining Mach numbers for supersonic flows.
∞ x=0 i
4.3.2 The subsonic Mach number may be determined from
4.3 Mach Number Determination:
4.3.1 TheMachnumberofastreamisafunctionofthetotal Fig.3(seealsoTestMethodE511).Aniterationisnecessaryto
determine the Mach number since the ratio of specific heats,γ,
enthalpy, the ratio of freestream pressure to the total pressure,
p/p ,thetotalpressure, p ,andtheratiooftheexitnozzlearea is also a function of enthalpy and pressure.
t t
1 1
FIG. 2 (a) Variation of Area Ratio with Mach Numbers
E637 − 05 (2011)
FIG. 2 (b) Variation of Area Ratio with Mach Numbers (continued)
FIG. 3 Subsonic Pressure Ratio as a Function of Mach Number and γ
E637 − 05 (2011)
FIG. 4 Isentropic Exponent for Air in Equilibrium
4.3.3 Theratioofspecificheats,γ,isshownasafunctionof 4.6.2 The proper application requires some knowledge of
entropy and enthalpy for air in Fig. 4 from Ref (9). S/R is the
the radiant environment in the stream at the desired operating
dimensionless entropy, and H/RT is the dimensionless en-
conditions. Usually, it is necessary to measure the radiant heat
thalpy.
transfer rate either directly or indirectly.The following is a list
of suggested methods by which the necessary measurements
4.4 Velocity Gradient Calculation from Pressure
can be made.
Distribution—The dimensionless stagnation-point velocity
gradient may be obtained from an experimentally measured 4.6.2.1 Direct Measurement with Radiometer—Radiometers
pressure distribution by using Bernoulli’s compressible flow
are available for the measurement of the incident radiant flux
equation as follows:
while excluding the convective heat transfer. In its simplest
γ21 0.5
form, the radiometer is a slug, thin-skin, or circular foil
@1 2 p/p γ #
U ~ !
t
5 (7) calorimeter with a sensing area with a coating of known
S D
γ21 0.5
U
`
1 2 p /p γ
@ ~ ! #
` t
2 absorptance and covered with some form of window. The
purpose of the window is to prevent convective heat transfer
where the velocity ratio may be calculated along the body
from affecting the calorimeter while transmitting the radiant
from the stagnation point. Thus, the dimensionless stagnation-
energy.Thewindowisusuallymadeofquartzorsapphire.The
point velocity gradient, (βD/U ) , is the slope of the U/U
∞ x=0 ∞
sensing surface is at the stagnation point of a test probe and is
and the x/D curve at the stagnation point.
located in such a manner that the view angle is not restricted.
4.5 Model Shape—Thenondimensionalstagnation-pointve-
The basic radiometer view angle should be 120° or greater.
locity gradient is a function of the model shape and the Mach
This technique allows for immersion of the radiometer in the
number. For supersonic Mach numbers, the heat transfer
test stream and direct measurement of the radiant heat transfer
relationship between a hemisphere and other axisymmetric
rate. There is a major limitation to this technique, however, in
blunt bodies is shown in Fig. 5 (10).In Fig. 5, r is the corner
c
that even with high-pressure water cooling of the radiometer
radius, r isthebodyradius, r isthenoseradius,and q˙ isthe
b n s,h
enclosure, the window is poorly cooled and thus the use of
stagnation-point heat transfer rate on a hemisphere. For sub-
windows is limited to relatively low convective heat transfer
sonic Mach numbers, the same type of variation is shown in
conditions or very short exposure times, or both.Also, stream
Fig. 6(6).
contaminants coat the window and reduce its transmittance.
4.6 Radiation Effects:
4.6.2.2 Direct Measurement with Radiometer Mounted in
4.6.1 As this test method depends on the accurate determi-
Cavity—Thetwolimitationsnotedin4.6.2.1maybeovercome
nation of the convective stagnation-point heat transfer, any
by mounting the radiometer at the bottom of a cavity open to
radiant energy absorbed by the calorimeter surface and incor-
the stagnation point of the test probe (see Fig. 7). Good results
rectly attributed to the convective mode will directly affect the
can be obtained by using a simple calorimeter in place of the
overall accuracy of the test method. Generally, the sources of
radiometer with a material of known absorptance. When using
radiant energy are the hot gas stream itself or the gas heating
this configuration, the measured radiant heat transfer rate is
device, or both. For instance, arc heaters operated at high
pressure (10 atm or higher) can produce significant radiant used in the following equation to determine the stagnation-
point radiant heat transfer, assuming diffuse radiation:
fluxes at the nozzle exit plane.
E637 − 05 (2011)
FIG. 5 Stagnation-Point Heating-Rate Parameters on Hemispherical Segments of Different Curvatures for Varying Corner-Radius Ratios
E637 − 05 (2011)
FIG. 6 Stagnation-Point Heat Transfer Ratio to a Blunt Body and a Hemisphere as a Function of the
Body-to-Nose Radius in a Subsonic Stream
FIG. 7 Test Probe
2 2 2 1/2
1 F 51/2 X 2 X 2 4E D (9)
@ ~ ! #
q˙ 5 q˙ (8)
r r
1 2
α F
2 12
where:
q˙ = radiant transfer at
...

Questions, Comments and Discussion

Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.

This May Also Interest You

ASTM
ASTM E637-22(Test Method)
Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure

SIGNIFICANCE AND USE
3.1 The purpose of this test method is to provide a standard calculation of the stagnation enthalpy of an aerodynamic simulation device using the heat transfer theory and measured values of stagnation point heat transfer and pressure. A stagnation enthalpy obtained by this test method gives a consistent set of data, along with heat transfer and stagnation pressure for ablation computations.
SCOPE
1.1 This test method covers the calculation from heat transfer theory of the stagnation enthalpy from experimental measurements of the stagnation-point heat transfer and stagnation pressure.  
1.2 Advantages:  
1.2.1 A value of stagnation enthalpy can be obtained at the location in the stream where the model is tested. This value gives a consistent set of data, along with heat transfer and stagnation pressure, for ablation computations.  
1.2.2 This computation of stagnation enthalpy does not require the measurement of any arc heater parameters.  
1.3 Limitations and Considerations—There are many factors that may contribute to an error using this type of approach to calculate stagnation enthalpy, including:  
1.3.1 Turbulence—The turbulence generated by adding energy to the stream may cause deviation from the laminar equilibrium heat transfer theory.  
1.3.2 Equilibrium, Nonequilibrium, or Frozen State of Gas—The reaction rates and expansions may be such that the gas is far from thermodynamic equilibrium.  
1.3.3 Noncatalytic Effects—The surface recombination rates and the characteristics of the metallic calorimeter may give a heat transfer deviation from the equilibrium theory.  
1.3.4 Free Electric Currents—The arc-heated gas stream may have free electric currents that will contribute to measured experimental heat transfer rates.  
1.3.5 Nonuniform Pressure Profile—A nonuniform pressure profile in the region of the stream at the point of the heat transfer measurement could distort the stagnation point velocity gradient.  
1.3.6 Mach Number Effects—The nondimensional stagnation-point velocity gradient is a function of the Mach number. In addition, the Mach number is a function of enthalpy and pressure such that an iterative process is necessary.  
1.3.7 Model Shape—The nondimensional stagnation-point velocity gradient is a function of model shape.  
1.3.8 Radiation Effects—The hot gas stream may contribute a radiative component to the heat transfer rate.  
1.3.9 Heat Transfer Rate Measurement—An error may be made in the heat transfer measurement (see Method E469 and Test Methods E422, E457, E459, and E511).  
1.3.10 Contamination—The electrode material may be of a large enough percentage of the mass flow rate to contribute to the heat transfer rate measurement.  
1.4 Units—The values stated in SI units are to be regarded as standard. No other units of measurement are included in this standard.  
1.4.1 Exception—The values given in parentheses are for information only.  
1.5 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety, health, and environmental practices and determine the applicability of regulatory limitations prior to use.  
1.6 This international standard was developed in accordance with internationally recognized principles on standardization established in the Decision on Principles for the Development of International Standards, Guides and Recommendations issued by the World Trade Organization Technical Barriers to Trade (TBT) Committee.

  • Standard
    16 pages
    English language
    sale 15% off
  • Standard
    16 pages
    English language
    sale 15% off
ASTM
ASTM E459-22(Test Method)
Standard Test Method for Measuring Heat Transfer Rate Using a Thin-Skin Calorimeter

SIGNIFICANCE AND USE
5.1 This test method may be used to measure the net heat transfer rate to a metallic or coated metallic surface for a variety of applications, including:  
5.1.1 Measurements of aerodynamic heating when the calorimeter is placed into a flow environment, such as a wind tunnel or an arc jet; the calorimeters can be designed to have the same size and shape as the actual test specimens to minimize heat transfer corrections;  
5.1.2 Heat transfer measurements in fires and fire safety testing;  
5.1.3 Laser power and laser absorption measurements; as well as,  
5.1.4 X-ray and particle beam (electrons or ions) dosimetry measurements.  
5.2 The thin-skin calorimeter is one of many concepts used to measure heat transfer rates. It may be used to measure convective, radiative, or combinations of convective and radiative (usually called mixed or total) heat transfer rates. However, when the calorimeter is used to measure radiative or mixed heat transfer rates, the absorptivity and reflectivity of the surface should be measured over the expected radiation wavelength region of the source, and as functions of temperature if possible.  
5.3 In 6.6 and 6.7, it is demonstrated that lateral heat conduction effects on a local measurement can be minimized by using a calorimeter material with a low thermal conductivity. Alternatively, a distribution of the heat transfer rate may be obtained by placing a number of thermocouples along the back surface of the calorimeter.  
5.4 In high temperature or high heat transfer rate applications, the principal drawback to the use of thin-skin calorimeters is the short exposure time necessary to ensure survival of the calorimeter such that repeat measurements can be made with the same sensor. When operation to burnout is necessary to obtain the desired heat flux measurements, thin-skin calorimeters are often a good choice because they are relatively inexpensive to fabricate.  
5.5 It is important to understand that the calorimeter design (th...
SCOPE
1.1 This test method covers the design and use of a thin metallic calorimeter for measuring heat transfer rate (also called heat flux). Thermocouples are attached to the unexposed surface of the calorimeter. A one-dimensional heat flow analysis is used for calculating the heat transfer rate from the temperature measurements. Applications include aerodynamic heating, laser and radiation power measurements, and fire safety testing.  
1.2 Advantages:  
1.2.1 Simplicity of Construction—The calorimeter may be constructed from a number of materials. The size and shape can often be made to match the actual application. Thermocouples may be attached to the metal by spot, electron beam, or laser welding.  
1.2.2 Heat transfer rate distributions may be obtained if metals with low thermal conductivity, such as some stainless steels or Inconel 600, are used.  
1.2.3 The calorimeters can be fabricated with smooth surfaces, without insulators or plugs and the attendant temperature discontinuities, to provide more realistic flow conditions for aerodynamic heating measurements.  
1.2.4 The calorimeters described in this test method are relatively inexpensive. If necessary, they may be operated to burn-out to obtain heat transfer information.  
1.3 Limitations:  
1.3.1 At higher heat flux levels, short test times are necessary to ensure calorimeter survival.  
1.3.2 For applications in wind tunnels or arc-jet facilities, the calorimeter must be operated at pressures and temperatures such that the thin-skin does not distort under pressure loads. Distortion of the surface will introduce measurement errors.  
1.3.3 Interpretation of the heat flux estimated may require additional analysis if the thin-skin calorimeter configuration is different from the test specimen.  
1.4 Units—The values stated in SI units are to be regarded as standard. No other units of measurement are included in this standard.  
1.4.1 Exception—The values ...

  • Standard
    11 pages
    English language
    sale 15% off
  • Standard
    11 pages
    English language
    sale 15% off
ASTM
ASTM E422-22(Test Method)
Standard Test Method for Measuring Net Heat Flux Using a Water-Cooled Calorimeter

SIGNIFICANCE AND USE
5.1 The purpose of this test method is to measure the net heat flux to a water-cooled surface for purposes of calibration of the thermal environment into which test specimens are placed for evaluation. The measured net heat flux is one of the important parameters for correlating the behavior of materials. If the calorimeter and holder size, shape, and surface finish are identical to that of the test specimen, the measured net heat flux to the calorimeter is presumed to be the same as that to the sample's heated surface. If the calorimeter configuration (holder size, shape, finish, etc.) is not identical to that of the test specimen, then the measurement results may need to be modified to account for those differences. See Appendix X1.  
5.2 The water-cooled calorimeter is one of several calorimeter concepts used to measure net heat flux. The prime drawback is its long response time, that is, the time required to achieve steady-state operation. To calculate energy added to the coolant water, accurate measurements of the rise in coolant temperature are needed, all energy losses should be minimized, and steady-state conditions must exist both in the thermal environment and fluid flow of the calorimeter.  
5.3 Regardless of the source of energy input to the water-cooled calorimeter surface (radiative, convective, or combinations thereof) the measurement is averaged over the surface-active area of the calorimeter. If the water-cooled calorimeter is used to measure only radiative flux or combined convective-radiative net heat flux rates, then the surface reflectivity of the calorimeter shall be measured over the wavelength region of interest (depending on the source of radiant energy). If nonuniformities exist in the gas stream, a large surface area water-cooled calorimeter would tend to smooth or average any variations. Consequently, it is advisable that the size of the calorimeter be limited to relatively small surface areas and applied to where the net heat flux is u...
SCOPE
1.1 This test method covers the measurement of a steady net heat flux to a given water-cooled surface by means of a system energy balance.  
1.2 Units—The values stated in SI units are to be regarded as standard. No other units of measurement are included in this standard.  
1.3 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety, health, and environmental practices and determine the applicability of regulatory limitations prior to use.  
1.4 This international standard was developed in accordance with internationally recognized principles on standardization established in the Decision on Principles for the Development of International Standards, Guides and Recommendations issued by the World Trade Organization Technical Barriers to Trade (TBT) Committee.

  • Standard
    8 pages
    English language
    sale 15% off
  • Standard
    8 pages
    English language
    sale 15% off
ASTM
ASTM E457-08(2020)(Test Method)
Standard Test Method for Measuring Heat-Transfer Rate Using a Thermal Capacitance (Slug) Calorimeter

SIGNIFICANCE AND USE
4.1 The purpose of this test method is to measure the rate of thermal energy per unit area transferred into a known piece of material (slug) for purposes of calibrating the thermal environment into which test specimens are placed for evaluation. The calorimeter and holder size and shape should be identical to that of the test specimen. In this manner, the measured heat transfer rate to the calorimeter can be related to that experienced by the test specimen.  
4.2 The slug calorimeter is one of many calorimeter concepts used to measure heat transfer rate. This type of calorimeter is simple to fabricate, inexpensive, and readily installed since it is not water-cooled. The primary disadvantages are its short lifetime and relatively long cool-down time after exposure to the thermal environment. In measuring the heat transfer rate to the calorimeter, accurate measurement of the rate of rise in back-face temperature is imperative.  
4.3 In the evaluation of high-temperature materials, slug calorimeters are used to measure the heat transfer rate on various parts of the instrumented models, since heat transfer rate is one of the important parameters in evaluating the performance of ablative materials.  
4.4 Regardless of the source of thermal energy to the calorimeter (radiative, convective, or a combination thereof) the measurement is averaged over the calorimeter surface. If a significant percentage of the total thermal energy is radiative, consideration should be given to the emissivity of the slug surface. If non-uniformities exist in the input energy, the heat transfer rate calorimeter would tend to average these variations; therefore, the size of the sensing element (that is, the slug) should be limited to small diameters in order to measure local heat transfer rate values. Where large ablative samples are to be tested, it is recommended that a number of calorimeters be incorporated in the body of the test specimen such that a heat transfer rate distribution across...
SCOPE
1.1 This test method describes the measurement of heat transfer rate using a thermal capacitance-type calorimeter which assumes one-dimensional heat conduction into a cylindrical piece of material (slug) with known physical properties.  
1.2 The values stated in SI units are to be regarded as standard. No other units of measurement are included in this standard.
Note 1: For information see Test Methods E285, E422, E458, E459, and E511.  
1.3 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety, health, and environmental practices and determine the applicability of regulatory limitations prior to use.  
1.4 This international standard was developed in accordance with internationally recognized principles on standardization established in the Decision on Principles for the Development of International Standards, Guides and Recommendations issued by the World Trade Organization Technical Barriers to Trade (TBT) Committee.

  • Standard
    6 pages
    English language
    sale 15% off
ASTM
ASTM E598-08(2020)(Test Method)
Standard Test Method for Measuring Extreme Heat-Transfer Rates from High-Energy Environments Using a Transient, Null-Point Calorimeter

SIGNIFICANCE AND USE
5.1 The purpose of this test method is to measure extremely high heat-transfer rates to a body immersed in either a static environment or in a high velocity fluid stream. This is usually accomplished while preserving the structural integrity of the measurement device for multiple exposures during the measurement period. Heat-transfer rates ranging up to 2.84 × 102 MW/m2 (2.5 × 104 Btu/ft2-sec) (7) have been measured using null-point calorimeters. Use of copper null-point calorimeters provides a measuring system with good response time and maximum run time to sensor burnout (or ablation). Null-point calorimeters are normally made with sensor body diameters of 2.36 mm (0.093 in.) press-fitted into the nose of an axisymmetric model.  
5.2 Sources of error involving the null-point calorimeter in high heat-flux measurement applications are extensively discussed in Refs (3-7). In particular, it has been shown both analytically and experimentally that the thickness of the copper above the null-point cavity is critical. If the thickness is too great, the time response of the instrument will not be fast enough to pick up important flow characteristics. On the other hand, if the thickness is too small, the null-point calorimeter will indicate significantly larger (and time dependent) values than the input or incident heat flux. Therefore, all null-point calorimeters should be experimentally checked for proper time response and calibration before they are used. Although a calibration apparatus is not very difficult or expensive to fabricate, there is only one known system presently in existence (6 and 7). The design of null-point calorimeters can be accomplished from the data in this documentation. However, fabrication of these sensors is a difficult task. Since there is not presently a significant market for null-point calorimeters, commercial sources of these sensors are few. Fabrication details are generally regarded as proprietary information. Some users have developed me...
SCOPE
1.1 This test method covers the measurement of the heat-transfer rate or the heat flux to the surface of a solid body (test sample) using the measured transient temperature rise of a thermocouple located at the null point of a calorimeter that is installed in the body and is configured to simulate a semi-infinite solid. By definition the null point is a unique position on the axial centerline of a disturbed body which experiences the same transient temperature history as that on the surface of a solid body in the absence of the physical disturbance (hole) for the same heat-flux input.  
1.2 Null-point calorimeters have been used to measure high convective or radiant heat-transfer rates to bodies immersed in both flowing and static environments of air, nitrogen, carbon dioxide, helium, hydrogen, and mixtures of these and other gases. Flow velocities have ranged from zero (static) through subsonic to hypersonic, total flow enthalpies from 1.16 to greater than 4.65 × 101 MJ/kg (5 × 10 2 to greater than 2 × 104 Btu/lb.), and body pressures from 105 to greater than 1.5 × 107 Pa (atmospheric to greater than 1.5 × 102 atm). Measured heat-transfer rates have ranged from 5.68 to 2.84 × 102 MW/m2 (5 × 102 to 2.5 × 104 Btu/ft2-sec).  
1.3 The most common use of null-point calorimeters is to measure heat-transfer rates at the stagnation point of a solid body that is immersed in a high pressure, high enthalpy flowing gas stream, with the body axis usually oriented parallel to the flow axis (zero angle-of-attack). Use of null-point calorimeters at off-stagnation point locations and for angle-of-attack testing may pose special problems of calorimeter design and data interpretation.  
1.4 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety, health, and environmental practices and determine the appli...

  • Standard
    10 pages
    English language
    sale 15% off
ASTM
ASTM E458-08(2020)(Test Method)
Standard Test Method for Heat of Ablation

SIGNIFICANCE AND USE
4.1 General—The heat of ablation provides a measure of the ability of a material to serve as a heat protection element in a severe thermal environment. The parameter is a function of both the material and the environment to which it is subjected. It is therefore required that laboratory measurements of heat of ablation simulate the service environment as closely as possible. Some of the parameters affecting the heat of ablation are pressure, gas composition, heat transfer rate, mode of heat transfer, and gas enthalpy. As laboratory duplication of all parameters is usually difficult, the user of the data should consider the differences between the service and the test environments. Screening tests of various materials under simulated use conditions may be quite valuable even if all the service environmental parameters are not available. These tests are useful in material selection studies, materials development work, and many other areas.  
4.2 Steady-State Conditions—The nature of the definition of heat of ablation requires steady-state conditions. Variances from steady-state may be required in certain circumstances; however, it must be realized that transient phenomena make the values obtained functions of the test duration and therefore make material comparisons difficult.  
4.2.1 Temperature Requirements—In a steady-state condition, the temperature propagation into the material will move at the same velocity as the gas-ablation surface interface. A constant distance is maintained between the ablation surface and the isotherm representing the temperature front. Under steady-state ablation the mass loss and length change are linearly related.
   where:
  t  =  test time, s,   ρo  =  virgin material density, kg/m3,   δL  =   change in length or ablation depth, m,   ρc  =   char density, kg/m3, and   δc  =   char depth, m.  This relationship may be used to verify the existence of steady-state ablation in the tests of charring ablators.  
4.2.2 Exposure T...
SCOPE
1.1 This test method covers determination of the heat of ablation of materials subjected to thermal environments requiring the use of ablation as an energy dissipation process. Three concepts of the parameter are described and defined: cold wall, effective, and thermochemical heat of ablation.  
1.2 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety, health, and environmental practices and determine the applicability of regulatory limitations prior to use.  
1.3 This international standard was developed in accordance with internationally recognized principles on standardization established in the Decision on Principles for the Development of International Standards, Guides and Recommendations issued by the World Trade Organization Technical Barriers to Trade (TBT) Committee.

  • Standard
    7 pages
    English language
    sale 15% off
ASTM
ASTM E341-08(2020)(Practice)
Standard Practice for Measuring Plasma Arc Gas Enthalpy by Energy Balance

SIGNIFICANCE AND USE
3.1 The purpose of this practice is to measure the total or stagnation gas enthalpy of a plasma-arc gas stream in which nonreactive gases are heated by passage through an electrical discharge device during calibration tests of the system.  
3.2 The plasma arc represents one heat source for determining the performance of high temperature materials under simulated hyperthermal conditions. As such the total or stagnation enthalpy is one of the important parameters for correlating the behavior of ablation materials.  
3.3 The most direct method for obtaining a measure of total enthalpy, and one which can be performed simultaneously with each material test, if desired, is to perform an energy balance on the arc chamber. In addition, in making the energy balance, accurate measurements are needed since the efficiencies of some plasma generators are low (as low as 15 to 20 % or less in which case the enthalpy depends upon the difference of two quantities of nearly equal magnitude). Therefore, the accuracy of the measurements of the primary variables must be high, all energy losses must be correctly taken into account, and steady-state conditions must exist both in plasma performance and fluid flow.  
3.4 In particular it is noted that total enthalpy as determined by the energy balance technique is most useful if the plasma generator design minimizes coring effects. If nonuniformity exists the enthalpy determined by energy balance gives only the average for the entire plasma stream, whereas the local enthalpy experienced by a model in the core of the stream may be much higher. More precise methods are needed to measure local variations in total enthalpy.
SCOPE
1.1 This practice covers the measurement of total gas enthalpy of an electric-arc-heated gas stream by means of an overall system energy balance. This is sometimes referred to as a bulk enthalpy and represents an average energy content of the test stream which may differ from local values in the test stream.  
1.2 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety, health, and environmental practices and determine the applicability of regulatory limitations prior to use.  
1.3 This international standard was developed in accordance with internationally recognized principles on standardization established in the Decision on Principles for the Development of International Standards, Guides and Recommendations issued by the World Trade Organization Technical Barriers to Trade (TBT) Committee.

  • Standard
    5 pages
    English language
    sale 15% off
ASTM
ASTM E511-07(2020)(Test Method)
Standard Test Method for Measuring Heat Flux Using a Copper-Constantan Circular Foil, Heat-Flux Transducer

SIGNIFICANCE AND USE
3.1 Fig. 1 is a sectional view of an example circular foil heat-flux transducer. It consists of a circular Constantan foil attached by a metallic bonding process to a heat sink of oxygen-free high conductivity copper (OFHC), with copper leads attached at the center of the circular foil and at any point on the heat-sink body. The transducer impedance is usually less than 1 V. To minimize current flow, the data acquisition system (DAS) should be a potentiometric system or have an input impedance of at least 100 000 Ω.  
3.2 As noted in 2.3, an approximately linear output (versus heat flux) is produced when the body and center wire of the transducer are constructed of copper and the circular foil is constantan. Other metal combinations may be employed for use at higher temperatures, but most (4) are nonlinear.  
3.3 Because the thermocouple junction at the edge of the foil is the reference for the center thermocouple, no cold junction compensation is required with this instrument. The wire leads used to convey the signal from the transducer to the readout device are normally made of stranded, tinned copper, insulated with TFE-fluorocarbon and shielded with a braid over-wrap that is also TFE-fluorocarbon-covered.  
3.4 Transducers with a heat-sink thermocouple can be used to indicate the foil center temperature. Once the edge temperature is known, the temperature difference from the foil edge to its center may be directly read from the copper-constantan (Type T) thermocouple table. This temperature difference then is added to the body temperature, indicating the foil center temperature.  
3.5 Water-Cooled Transducer:  
3.5.1 A water-cooled transducer should be used in any application where the copper heat-sink would rise above 235 °C (450 °F) without cooling. Examples of cooled transducers are shown in Fig. 2. The coolant flow must be sufficient to prevent local boiling of the coolant inside the transducer body, with its characteristic pulsations (“chugging”) of t...
SCOPE
1.1 This test method describes the measurement of radiative heat flux using a transducer whose sensing element (1, 2)2 is a thin circular metal foil. These sensors are often called Gardon Gauges.  
1.2 The values stated in SI units are to be regarded as the standard. The values stated in parentheses are provided for information only.  
1.3 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety, health, and environmental practices and determine the applicability of regulatory limitations prior to use.  
1.4 This international standard was developed in accordance with internationally recognized principles on standardization established in the Decision on Principles for the Development of International Standards, Guides and Recommendations issued by the World Trade Organization Technical Barriers to Trade (TBT) Committee.

  • Standard
    11 pages
    English language
    sale 15% off
ASTM
ASTM E3057-19(Test Method)
Standard Test Method for Measuring Heat Flux Using Directional Flame Thermometers with Advanced Data Analysis Techniques

SIGNIFICANCE AND USE
5.1 Need for Heat Flux Measurements:  
5.1.1 Independent measurements of temperature and heat flux support the development and validation of engineering models of fires and other high environments, such as furnaces. For tests of fire protection materials and structural assemblies, temperature and heat flux are necessary to fully specify the boundary conditions, also known as the thermal exposure. Temperature measurements alone cannot provide a complete set of boundary conditions.  
5.1.2 Temperature is a scalar variable and a primary variable. Heat Flux is a vector quantity, and it is a derived variable. As a result, they should be measured separately just as current and voltage are in electrical systems. For steady-state or quasi-steady state conditions, analysis basically uses a thermal analog of Ohm's Law. The thermal circuit uses the temperature difference instead of voltage drop, the heat flux in place of the current and thermal resistance in place of electrical resistance. As with electrical systems, the thermal performance is not fully specified without knowing at least two of these three parameters (temperature drop, heat flux, or thermal resistance). For dynamic thermal experiments like fires or fire safety tests, the electrical capacitance is replaced by the volumetric heat capacity.  
5.1.3 The net heat flux, which is measured by a DFT, is likely different than the heat flux into the test item of interest because of different surface temperatures. An alternative measurement is the total cold wall heat flux which is measured by water-cooled Gardon or S-B gauges. The incident radiative flux can be estimated from either measurement by use of an energy balance [Keltner, 2007 and 2008 (16, 17)]. The convective flux can be estimated from gas temperatures and the convective heat transfer coefficient, h [Janssens, 2007 (18)]. Assuming the sensor is physically close to the test item of interest; one can use the incident radiative and convective fluxes from the...
SCOPE
1.1 This test method describes the continuous measurement of the hemispherical heat flux to one or both surfaces of an uncooled sensor called a “Directional Flame Thermometer” (DFT).  
1.2 DFTs consist of two heavily oxidized, Inconel 600 plates with mineral insulated, metal-sheathed (MIMS) thermocouples (TCs, type K) attached to the unexposed faces and a layer of ceramic fiber insulation placed between the plates.  
1.3 Post-test calculations of the net heat flux can be made using several methods. The most accurate method uses an inverse heat conduction code. Nonlinear inverse heat conduction analysis uses a thermal model of the DFT with temperature dependent thermal properties along with the two plate temperature measurement histories. The code provides transient heat flux on both exposed faces, temperature histories within the DFT as well as statistical information on the quality of the analysis.  
1.4 A second method uses a transient energy balance on the DFT sensing surface and insulation, which uses the same temperature measurements as in the inverse calculations to estimate the net heat flux.  
1.5 A third method uses Inverse Filter Functions (IFFs) to provide a near real time estimate of the net flux. The heat flux history for the “front face” (either surface exposed to the heat source) of a DFT can be calculated in real-time using a convolution type of digital filter algorithm.  
1.6 Although developed for use in fires and fire safety testing, this measurement method is quite broad in potential fields of application because of the size of the DFTs and their construction. It has been used to measure heat flux levels above 300 kW/m2 in high temperature environments, up to about 1250 °C, which is the generally accepted upper limit of Type K or N thermocouples.  
1.7 The transient response of the DFTs is limited by the response of the MIMS TCs. The larger the thermocouple the slower the transient response. Res...

  • Standard
    25 pages
    English language
    sale 15% off
  • Standard
    25 pages
    English language
    sale 15% off
ASTM
ASTM E2684-17(Test Method)
Standard Test Method for Measuring Heat Flux Using Surface-Mounted One-Dimensional Flat Gages

SIGNIFICANCE AND USE
5.1 This test method will provide guidance for the measurement of the net heat flux to or from a surface location. To determine the radiant energy component the emissivity or absorptivity of the gage surface coating is required and should be matched with the surrounding surface. The potential physical and thermal disruptions of the surface due to the presence of the gage should be minimized and characterized. For the case of convection and low source temperature radiation to or from the surface it is important to consider how the presence of the gage alters the surface heat flux. The desired quantity is usually the heat flux at the surface location without the presence of the gage.  
5.1.1 Temperature limitations are determined by the gage material properties and the method of application to the surface. The range of heat flux that can be measured and the time response are limited by the gage design and construction details. Measurements from 10 W/m2 to above 100 kW/m2 are easily obtained with current sensors. Time constants as low as 10 ms are possible, while thicker sensors may have response times greater than 1 s. It is important to choose the sensor style and characteristics to match the range and time response of the required application.  
5.2 The measured heat flux is based on one-dimensional analysis with a uniform heat flux over the surface of the gage surface. Because of the thermal disruption caused by the placement of the gage on the surface, this may not be true. Wesley (3) and Baba et al. (4) have analyzed the effect of the gage on the thermal field and heat transfer within the surface substrate and determined that the one-dimensional assumption is valid when:
   where:
  ks  =   the thermal conductivity of the substrate material,    R   =  the effective radius of the gage,    δ  =  the combined thickness, and     k  =  the effective thermal conductivity of the gage and adhesive layers.    
5.3 Measurements of convective heat flux are part...
SCOPE
1.1 This test method describes the measurement of the net heat flux normal to a surface using flat gages mounted onto the surface. Conduction heat flux is not the focus of this standard. Conduction applications related to insulation materials are covered by Test Method C518 and Practices C1041 and C1046. The sensors covered by this test method all use a measurement of the temperature difference between two parallel planes normal to the surface to determine the heat that is exchanged to or from the surface in keeping with Fourier’s Law. The gages operate by the same principles for heat transfer in either direction.  
1.2 This test method is quite broad in its field of application, size and construction. Different sensor types are described in detail in later sections as examples of the general method for measuring heat flux from the temperature gradient normal to a surface (1).2 Applications include both radiation and convection heat transfer. The gages have broad application from aerospace to biomedical engineering with measurements ranging form 0.01 to 50 kW/m 2. The gages are usually square or rectangular and vary in size from 1 mm to 10 cm or more on a side. The thicknesses range from 0.05 to 3 mm.  
1.3 The values stated in SI units are to be regarded as the standard. The values stated in parentheses are provided for information only.  
1.4 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.  
1.5 This international standard was developed in accordance with internationally recognized principles on standardization established in the Decision on Principles for the Development of International Standards, Guides and Recommendations issued by the World Trade Organization Technical Barriers to...

  • Standard
    7 pages
    English language
    sale 15% off
  • Standard
    7 pages
    English language
    sale 15% off