ASTM E637-05

Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure

SIGNIFICANCE AND USE
The purpose of this test method is to provide a standard calculation of the stagnation enthalpy of an aerodynamic simulation device using the heat transfer theory and measured values of stagnation point heat transfer and pressure. A stagnation enthalpy obtained by this test method gives a consistent set of data, along with heat transfer and stagnation pressure for ablation computations.
SCOPE
1.1 This test method covers the calculation from heat transfer theory of the stagnation enthalpy from experimental measurements of the stagnation-point heat transfer and stagnation pressure.
1.2 Advantages
1.2.1 A value of stagnation enthalpy can be obtained at the location in the stream where the model is tested. This value gives a consistent set of data, along with heat transfer and stagnation pressure, for ablation computations.
1.2.2 This computation of stagnation enthalpy does not require the measurement of any arc heater parameters.
1.3 Limitations and ConsiderationsThere are many factors that may contribute to an error using this type of approach to calculate stagnation enthalpy, including:
1.3.1 TurbulenceThe turbulence generated by adding energy to the stream may cause deviation from the laminar equilibrium heat transfer theory.
1.3.2 Equilibrium, Nonequilibrium, or Frozen State of GasThe reaction rates and expansions may be such that the gas is far from thermodynamic equilibrium.
1.3.3 Noncatalytic EffectsThe surface recombination rates and the characteristics of the metallic calorimeter may give a heat transfer deviation from the equilibrium theory.
1.3.4 Free Electric CurrentsThe arc-heated gas stream may have free electric currents that will contribute to measured experimental heat transfer rates.
1.3.5 Nonuniform Pressure ProfileA nonuniform pressure profile in the region of the stream at the point of the heat transfer measurement could distort the stagnation point velocity gradient.
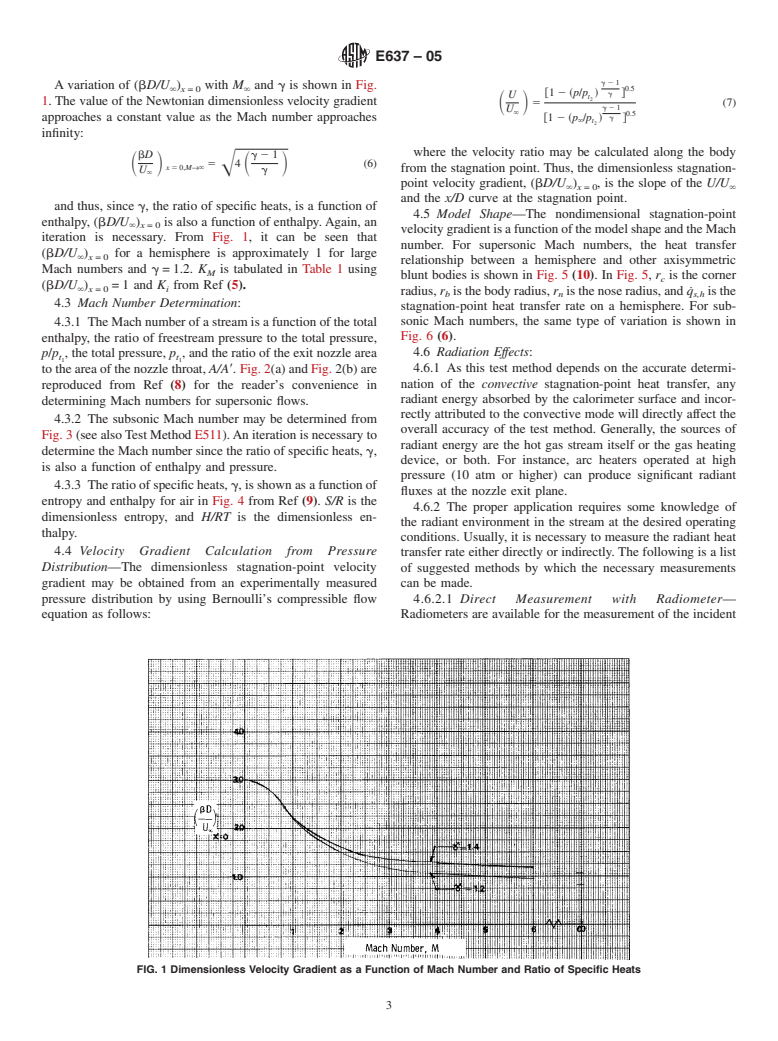
1.3.6 Mach Number EffectsThe nondimensional stagnation-point velocity gradient is a function of the Mach number. In addition, the Mach number is a function of enthalpy and pressure such that an iterative process is necessary.
1.3.7 Model ShapeThe nondimensional stagnation-point velocity gradient is a function of model shape.
1.3.8 Radiation EffectsThe hot gas stream may contribute a radiative component to the heat transfer rate.
1.3.9 Heat Transfer Rate Measurement An error may be made in the heat transfer measurement (see Method E 469 and Test Methods E 422, E 457, E 459, and E 511).
1.3.10 ContaminationThe electrode material may be of a large enough percentage of the mass flow rate to contribute to the heat transfer rate measurement.
1.4 The values stated in SI units are to be regarded as the standard. The values given in parentheses are for information only.
This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.

General Information

• Status: Historical
• Publication Date: 14-Sep-2005
• Technical Committee: E21 - Space Simulation and Applications of Space Technology
• Drafting Committee: E21.08 - Thermal Protection

Relations

• Replaces: ASTM E637-98 - Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure
• Effective Date: 15-Sep-2005
• Replaced By: ASTM E637-05(2011) - Standard Test Method for Calculation of Stagnation Enthalpy from Heat Transfer Theory and Experimental Measurements of Stagnation-Point Heat Transfer and Pressure
• Effective Date: 01-Oct-2011

Standards Content (Sample)

NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E637 – 05
Standard Test Method for
Calculation of Stagnation Enthalpy from Heat Transfer
Theory and Experimental Measurements of Stagnation-Point
1
Heat Transfer and Pressure
This standard is issued under the fixed designation E637; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
INTRODUCTION
The enthalpy (energy per unit mass) determination in a hot gas aerodynamic simulation device is
a difficult measurement. Even at temperatures that can be measured with thermocouples, there are
many corrections to be made at 600 K and above. Methods that are used for temperatures above the
range of thermocouples that give bulk or average enthalpy values are energy balance (see Practice
2
E341), sonic flow (1, 2), and the pressure rise method (3). Local enthalpy values (thus distribution)
may be obtained by using either an energy balance probe (see Method E470), or the spectrometric
technique described in Ref (4).
1. Scope 1.3.2 Equilibrium, Nonequilibrium, or Frozen State of
Gas—The reaction rates and expansions may be such that the
1.1 This test method covers the calculation from heat
gas is far from thermodynamic equilibrium.
transfer theory of the stagnation enthalpy from experimental
1.3.3 Noncatalytic Effects—The surface recombination
measurements of the stagnation-point heat transfer and stagna-
rates and the characteristics of the metallic calorimeter may
tion pressure.
give a heat transfer deviation from the equilibrium theory.
1.2 Advantages:
1.3.4 Free Electric Currents—The arc-heated gas stream
1.2.1 Avalue of stagnation enthalpy can be obtained at the
mayhavefreeelectriccurrentsthatwillcontributetomeasured
location in the stream where the model is tested. This value
experimental heat transfer rates.
gives a consistent set of data, along with heat transfer and
1.3.5 Nonuniform Pressure Profile—Anonuniformpressure
stagnation pressure, for ablation computations.
profile in the region of the stream at the point of the heat
1.2.2 This computation of stagnation enthalpy does not
transfer measurement could distort the stagnation point veloc-
require the measurement of any arc heater parameters.
ity gradient.
1.3 Limitations and Considerations—There are many fac-
1.3.6 Mach Number Effects—The nondimensional
tors that may contribute to an error using this type of approach
stagnation-point velocity gradient is a function of the Mach
to calculate stagnation enthalpy, including:
number.Inaddition,theMachnumberisafunctionofenthalpy
1.3.1 Turbulence—The turbulence generated by adding en-
and pressure such that an iterative process is necessary.
ergy to the stream may cause deviation from the laminar
1.3.7 Model Shape—The nondimensional stagnation-point
equilibrium heat transfer theory.
velocity gradient is a function of model shape.
1.3.8 Radiation Effects—Thehotgasstreammaycontribute
a radiative component to the heat transfer rate.
1
This test method is under the jurisdiction of ASTM Committee E21 on Space
1.3.9 Heat Transfer Rate Measurement—An error may be
Simulation andApplications of SpaceTechnology and is the direct responsibility of
made in the heat transfer measurement (see Method E469 and
Subcommittee E21.08 on Thermal Protection.
Current edition approved Sept. 15, 2005. Published November 2005. Originally
Test Methods E422, E457, E459, and E511).
approved in 1978. Last previous edition approved in 1998 as E637–98. DOI:
1.3.10 Contamination—The electrode material may be of a
10.1520/E0637-05.
2
large enough percentage of the mass flow rate to contribute to
The boldface numbers in parentheses refer to the list of references appended to
this method. the heat transfer rate measurement.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
1

---------------------- Page: 1 ----------------------
E637 – 05
1.4 The values stated in SI units are to be regarded as the
H = wall enthalpy, J/kg (or Btu/lb), and
w
standard. The values given in parentheses are for information
K = heat transfer computation constant.
i
only.
4.2 Low Mach Number Correction—Eq 1 is simple and
1.5 This standard does not purport to address all of the
convenient to use since K can be considered approximately
i
safety concerns, if any, associated with its use. It is the
constant(seeTable1).However,Eq1isbasedonastagnation-
responsibility of the user of this standard to establish appro-
point velocity gradient derived using “modified” Newtonian
priate safety and health practices and determine the applica-
flow theory which becomes inaccurate for M <2.An
oo
bility of regulato
...