ASTM E2586-07
(Practice)Standard Practice for Calculating and Using Basic Statistics
Standard Practice for Calculating and Using Basic Statistics
SCOPE
1.1 This practice covers methods and formulas for computing and presenting basic descriptive statistics using a set of sample data containing a single variable. This practice includes simple descriptive statistics for variable data, tabular and graphical methods for variable data, and methods for summarizing simple attribute data. Some interpretation and guidance for use is also included.
1.2 The system of units for this Practice is not specified. Dimensional quantities in the Practice are presented only as illustrations of calculation methods. The examples are not binding on products or test methods treated.
This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation:E2586–07
Standard Practice for
Calculating and Using Basic Statistics
This standard is issued under the fixed designation E2586; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope 3.1.1 coeffıcient of variation,CV, n—foranonnegativechar-
acteristic, the ratio of the standard deviation to the mean for a
1.1 This practice covers methods and formulas for comput-
population or sample
ing and presenting basic descriptive statistics using a set of
3.1.1.1 Discussion—The coefficient of variation is often
sampledatacontainingasinglevariable.Thispracticeincludes
expressed as a percentage.
simple descriptive statistics for variable data, tabular and
3.1.1.2 Discussion—This statistic is also known as the
graphical methods for variable data, and methods for summa-
relative standard deviation, RSD.
rizing simple attribute data. Some interpretation and guidance
3.1.2 characteristic, n—a property of items in a sample or
for use is also included.
population which, when measured, counted, or otherwise
1.2 The system of units for this practice is not specified.
observed, helps to distinguish among the items. E2282
Dimensional quantities in the Practice are presented only as
3.1.3 empirical percentile, n—estimate of a population
illustrations of calculation methods. The examples are not
percentile using the sample data. This is a sample value such
binding on products or test methods treated.
that a percentage p of the sample is less than that value.
1.3 This standard does not purport to address all of the
3.1.4 histogram, n—graphical representation of the fre-
safety concerns, if any, associated with its use. It is the
quency distribution of a characteristic consisting of a set of
responsibility of the user of this standard to establish appro-
rectangles with area proportional to the frequency.
priate safety and health practices and determine the applica-
ISO 3534-1
bility of regulatory limitations prior to use.
3.1.4.1 Discussion—While not required, equal bar or class
2. Referenced Documents
widths are recommended for histograms.
th
3.1.5 interquartile range, IQR, n—the 75 percentile (0.75
2.1 ASTM Standards:
th
quantile) minus the 25 percentile (0.25 quantile), for a data
E178 Practice for Dealing With Outlying Observations
set.
E456 Terminology Relating to Quality and Statistics
3.1.6 kurtosis, g,g , n—for a population or a sample, a
E2282 Guide for Defining the Test Result of a Test Method 2 2
measure of the weight of the tails of a distribution relative to
2.2 ISO Standards
the center, calculated as the ratio of the fourth central moment
ISO 3534-1 Statistics—Vocabulary and Symbols, part 1:
(empiricalifasample,theoreticalifapopulationapplies)tothe
Probability and General Statistical Terms
standard deviation (sample, s, or population, s) raised to the
ISO 3534-2 Statistics—Vocabulary and Symbols, part 2:
fourth power, minus 3 (also referred to as excess kurtosis).
Applied Statistics
3.1.7 mean, n—of a population, µ, average or expected
3. Terminology
value of a characteristic in a population – of a sample, x, sum
of the observed values in the sample divided by the sample
3.1 Definitions: Unless otherwise noted, terms relating to
size.
quality and statistics are as defined in Terminology E456.
th
3.1.8 median, X, n—the 50 percentile in a population or
sample.
This practice is under the jurisdiction ofASTM Committee E11 on Quality and
3.1.8.1 Discussion—The sample median is the [(n+1)/2]
Statistics and is the direct responsibility of Subcommittee E11.10 on Sampling /
order statistic if the sample size n is odd and is the average of
Statistics.
the [n/2] and [n/2+1] order statistics if n is even.
Current edition approved Oct. 1, 2007. Published November 2007. DOI:
10.1520/E2586-07.
3.1.9 midrange, n—average of the minimum and maximum
For referenced ASTM standards, visit the ASTM website, www.astm.org, or
values in a sample.
contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
th
3.1.10 order statistic, x , n—value of the k observed
Standards volume information, refer to the standard’s Document Summary page on (k)
the ASTM website. value in a sample after sorting by order of magnitude.
Available fromAmerican National Standards Institute (ANSI), 25 W. 43rd St.,
4th Floor, New York, NY 10036, http://www.ansi.org.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
E2586–07
3.1.10.1 Discussion—For a sample of size n, the first order dynamic, continuing to emerge and possibly change over time.
statistic x is the minimum value, x is the maximum value. Sample data serve as representatives of the population from
(1) (n)
3.1.11 population parameter, n—summary measure of the
which the sample originates. It is the population that is of
values of some characteristic of a population ISO 3534-2
primary interest in any particular study.
3.1.12 population, n—the totality of items or units of
4.2 The data (measurements and observations) may be of
material under consideration.
the variable type or the simple attribute type. In the case of
3.1.13 quantile,n—valuesuchthatafractionfofthesample
attributes, the data may be either binary trials or a count of a
or population is less than or equal to that value
defined event over some interval (time, space, volume, weight,
3.1.14 range, R, n—maximum value minus the minimum
or area). Binary trials consist of a sequence of 0s and 1s in
value in a sample.
which a “1” indicates that the inspected item exhibited the
3.1.15 sample, n—a group of observations or test results,
attribute being studied and a “0” indicates the item did not
taken from a larger collection of observations or test results,
exhibit the attribute. Each inspection item is assigned either a
whichservestoprovideinformationthatmaybeusedasabasis
“0” or a “1.” Such data are often governed by the binomial
for making a decision concerning the larger collection.
distribution. For a count of events over some interval, the
3.1.16 sample size, n, n—number of observed values in the
number of times the event is observed on the inspection
sample
interval is recorded for each of n inspection intervals. The
3.1.17 sample statistic, n—summary measure of the ob-
Poisson distribution often governs counting events over an
served values of a sample.
interval.
3.1.18 skewness, g,g , n—for population or sample, a
1 1
4.3 For sample data to be used to draw conclusions about
measure of symmetry of a distribution, calculated as the ratio
the population, the process of sampling and data collection
of the third central moment (empirical if a sample, and
must be considered, at least potentially, repeatable. Descriptive
theoretical if a population applies) to the standard deviation
statistics are calculated using real sample data that will vary in
(sample, s, or population, s) raised to the third power.
repeating the sampling process.As such, a statistic is a random
3.1.19 standard deviation—of a population, s, the square
variable subject to variation in its own right. The sample
root of the average or expected value of the squared deviation
statistic usually has a corresponding parameter in the popula-
of a variable from its mean – of a sample s , the square root of
tion that is unknown (see Section 5). The point of using a
the sum of the squared deviations of the observed values in the
sample divided by the sample size minus 1. statisticistosummarizethedatasetandestimateacorrespond-
2 2
ing population characteristic or parameter.
3.1.20 variance, s,s , n—square of the standard deviation
of the population or sample.
4.4 Descriptive statistics consider numerical, tabular, and
3.1.20.1 Discussion—For a finite population, s is calcu-
graphical methods for summarizing a set of data. The methods
latedasthesumofsquareddeviationsofvaluesfromthemean,
considered in this practice are used for summarizing the
divided by n. For a continuous population, s is calculated by
observations from a single variable.
integrating (x-µ) with respect to the density function. For a
4.5 The descriptive statistics described in this practice are:
sample, s is calculated as the sum of the squared deviations of
4.5.1 Mean, median, min, max, range, mid range, order
observedvaluesfromtheiraveragedividedbyonelessthanthe
statistic, quartile, empirical percentile, quantile, interquartile
sample size.
range, variance, standard deviation, Z-score, coefficient of
3.1.21 Z-score, n—observed value minus the sample mean
variation, skewness and kurtosis, and standard error.
divided by the sample standard deviation.
4.6 Tabular methods described in this practice are:
4. Significance and Use
4.6.1 Frequency distribution, relative frequency distribu-
4.1 This practice provides approaches for characterizing a
tion, cumulative frequency distribution, and cumulative rela-
sample of n observations that arrive in the form of a data set.
tive frequency distribution.
Large data sets from organizations, businesses, and govern-
4.7 Graphical methods described in this practice are:
mental agencies exist in the form of records and other
4.7.1 Histogram,ogive,boxplot,dotplot,normalprobability
empirical observations. Research institutions and laboratories
plot, and q-q plot.
at universities, government agencies, and the private sector
4.8 While the methods described in this practice may be
also generate considerable amounts of empirical data.
used to summarize any set of observations, the results obtained
4.1.1 Adata set containing a single variable usually consists
by using them may be of little value from the standpoint of
of a column of numbers. Each row is a separate observation or
interpretation unless the data quality is acceptable and satisfies
instance of measurement of the variable. The numbers them-
certain requirements.To be useful for inductive generalization,
selvesaretheresultofapplyingthemeasurementprocesstothe
any sample of observations that is treated as a single group for
variable being studied or observed. We may refer to each
presentationpurposesmustrepresentaseriesofmeasurements,
observation of a variable as an item in the data set. In many
all made under essentially the same test conditions, on a
situations, there may be several variables defined for study.
material or product, all of which have been produced under
4.1.2 The sample is selected from a larger set called the
population. The population can be a finite set of items, a very essentially the same conditions. When these criteria are met,
we are minimizing the danger of mixing two or more distinctly
large or essentially unlimited set of items, or a process. In a
process, the items originate over time and the population is different sets of data.
E2586–07
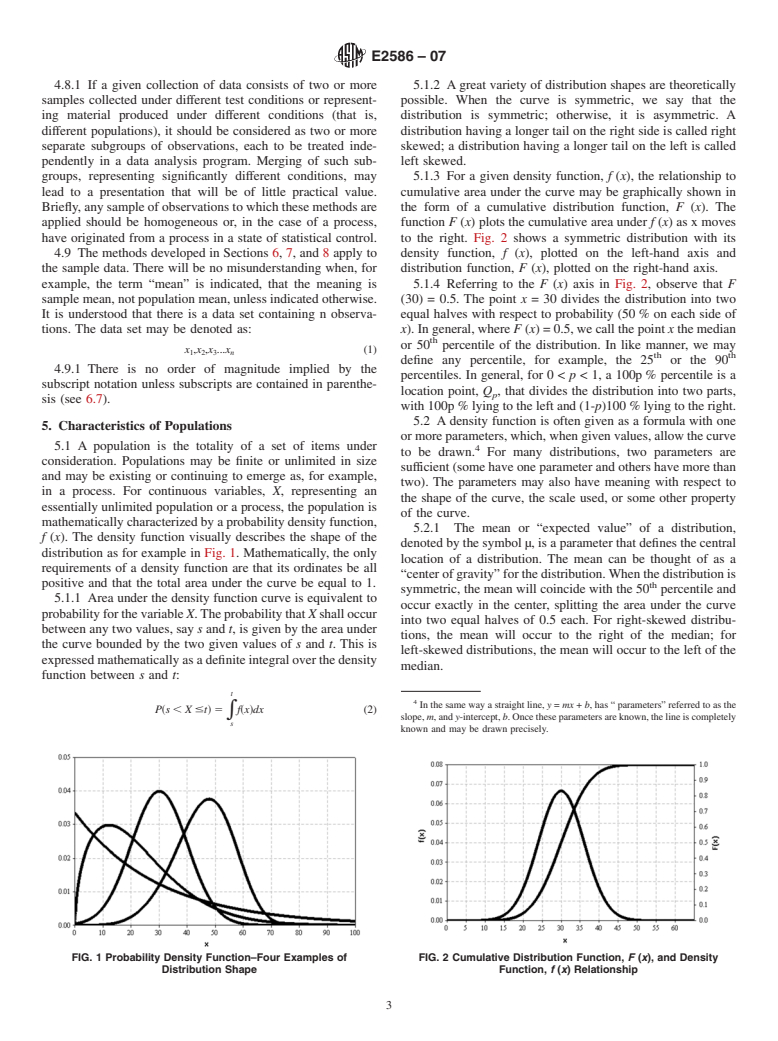
4.8.1 If a given collection of data consists of two or more 5.1.2 Agreat variety of distribution shapes are theoretically
samples collected under different test conditions or represent- possible. When the curve is symmetric, we say that the
ing material produced under different conditions (that is, distribution is symmetric; otherwise, it is asymmetric. A
different populations), it should be considered as two or more distribution having a longer tail on the right side is called right
separate subgroups of observations, each to be treated inde- skewed; a distribution having a longer tail on the left is called
pendently in a data analysis program. Merging of such sub- left skewed.
groups, representing significantly different conditions, may 5.1.3 For a given density function, f (x), the relationship to
lead to a presentation that will be of little practical value. cumulative area under the curve may be graphically shown in
Briefly, any sample of observations to which these methods are the form of a cumulative distribution function, F (x). The
applied should be homogeneous or, in the case of a process, function F (x) plots the cumulative area under f (x) as x moves
have originated from a process in a state of statistical control. to the right. Fig. 2 shows a symmetric distribution with its
4.9 The methods developed in Sections 6, 7, and 8 apply to density function, f (x), plotted on the left-hand axis and
the sample data. There will be no misunderstanding when, for distribution function, F (x), plotted on the right-hand axis.
example, the term “mean” is indicated, that the meaning is 5.1.4 Referring to the F (x) axis in Fig. 2, observe that F
samplemean,notpopulationmean,unlessindicatedotherwise. (30) = 0.5. The point x = 30 divides the distribution into two
It is understood that there is a data set containing n observa- equal halves with respect to probability (50 % on each side of
tions. The data set may be denoted as: x). In general, where F (x) = 0.5, we call the point x the median
th
or 50 percentile of the distribution. In like manner, we may
x ,x ,x .x (1)
1 2 3 n
th th
define any percentile, for example, the 25 or the 90
4.9.1 There is no order of magnitude implied by the
percentiles. In general, for 0 < p < 1, a 100p % percentile is a
subscript notation unless subscripts are contained in parenthe-
location point, Q , that divides the distribution into two parts,
p
sis (see 6.7).
with 100p % lying to the left and (1-p)100 % lying to the right.
5.2 A density function is often given as a formula with one
5. Characteristics of Populations
ormoreparameters,which,whengivenvalues,allowthecurve
5.1 A population is the totality of a set of items under
to be drawn. For many distributions, two parameters are
consideration. Populations may be finite or unlimited in size
sufficient (some have one parameter and others have more than
and may be existing or continuing to emerge as, for example,
two). The parameters may also have meaning with respect to
in a process. For continuous variables, X, representing an
the shape of the curve, the scale used, or some other property
essentially unlimited population or a process, the population is
of the curve.
mathematicallycharacterizedbyaprobabilitydensityfunction,
5.2.1 The mean or “expected value” of a distribution,
f (x). The density function visually describes the shape of the
denoted by the symbol µ, is a parameter that defines the central
distribution as for example in Fig. 1. Mathematically, the only
location of a distribution. The mean can be thought of as a
requirements of a density function are that its ordinates be all
“centerofgravity”forthedistribution.Whenthedistributionis
positive and that the total area under the
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.