ASTM E1561-93(1998)

Standard Practice for Analysis of Strain Gage Rosette Data

SCOPE
1.1 The two primary uses of three-element strain gage rosettes are (a) to determine the directions and magnitudes of the principal surface strains and (b) to determine residual stresses. Residual stresses are treated in a separate ASTM standard, Test Method E837. This practice defines a reference axis for each of the two principal types of rosette configurations used and presents equations for data analysis. This is important for consistency in reporting results and for avoiding ambiguity in data analysis-especially when computers are used. There are several possible sets of equations, but the set presented here is perhaps the most common.

General Information

• Status: Historical
• Publication Date: 09-Apr-1998
• ICS: 77.040.99 - Other methods of testing of metals
• Technical Committee: E28 - Mechanical Testing

Relations

• Replaced By: ASTM E1561-93(2003) - Standard Practice for Analysis of Strain Gage Rosette Data
• Effective Date: 10-Jun-2003
• Referred By: ASTM E998-19 - Standard Test Method for Structural Performance of Architectural Glass Products Under the Influence of Uniform Static Loads
• Effective Date: 10-Apr-1998

Standards Content (Sample)

NOTICE: This standard has either been superceded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
Designation: E 1561 – 93 (Reapproved 1998)
Standard Practice for
Analysis of Strain Gage Rosette Data
This standard is issued under the fixed designation E 1561; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
INTRODUCTION
There can be considerable confusion in interpreting and reporting the results of calculations
involving strain gage rosettes, particularly when data are exchanged between different laboratories.
Thus, it is necessary that users adopt a common convention for identifying the positions of the gages
and for analyzing the data.
1. Scope
1.1 The two primary uses of three-element strain gage
rosettes are (a) to determine the directions and magnitudes of
the principal surface strains and (b) to determine residual
stresses. Residual stresses are treated in a separate ASTM
standard, Test Method E 837. This practice defines a reference
axis for each of the two principal types of rosette configura-
tions used and presents equations for data analysis. This is
important for consistency in reporting results and for avoiding
ambiguity in data analysis—especially when computers are
used. There are several possible sets of equations, but the set
presented here is perhaps the most common.
FIG. 1 0° – 45° – 90° Rosette
2. Referenced Documents
After corrections for thermal effects and transverse sensitivity
2.1 ASTM Standards:
have been made, the measured strains represent the surface
E 6 Terminology Relating to Methods of Mechanical Test-
strains at the site of the rosette. It is assumed here that the
ing
elastic modulus and thickness of the test specimen are such that
E 837 Test Method for Determining Residual Stresses by
mechanical reinforcement by the rosette are negligible. For test
the Hole-Drilling Strain-Gage Method
objects subjected to unknown combinations of bending and
direct (membrane) stresses, the separate bending and mem-
3. Terminology
brane stresses can be obtained as shown in 4.4.
3.1 The terms in Terminology E 6 apply.
3.2.4 e8 , e8 , e8 —reduced membrane strain components
a b c
3.2 Additional terms and notation are as follows:
(4.4).
3.2.1 reference line—the axis of the a gage.
3.2.2 a, b, c—the three-strain gages making up the rosette.
For the 0° – 45° – 90° rosette (Fig. 1) the axis of the b gage is
located 45° counterclockwise from the a (reference line) axis
and the c gage is located 90° counterclockwise from the a axis.
For the 0° – 60° – 120° rosette (Fig. 2) the axis of the b gage is
located 60° counterclockwise from the a axis and the c axis is
located 120° counterclockwise from the a axis.
3.2.3 e , e ,e —the strains measured by gages a, b, and c,
a b c
respectively, positive in tension and negative in compression.
This practice is under the jurisdiction of ASTM Committee E-28 on Mechanical
Testing and is the direct responsibility of Subcommittee E28.14 on Strain Gages.
Current edition approved Aug. 15, 1993. Published October 1993.
Annual Book of ASTM Standards, Vol 03.01. FIG. 2 0° – 60° – 120° Rosette
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
NOTICE: This standard has either been superceded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
E 1561
3.2.5 e9 , e9 ,e9 —reduced bending strain components (4.4).
a b c
3.2.6 e —the calculated maximum (more tensile or less
compressive) principal strain.
3.2.7 e —the calculated minimum (less tensile or more
compressive) principal strain.
3.2.8 g —the calculated maximum shear strain.
M
3.2.9 u —the angle from the reference line to the direction
of e . This angle is less than or equal to 180° in magnitude.
FIG. 4 Differential Element on the Undeformed Surface
3.2.10 C, R—values used in the calculations. C is the
location, along the e-axis, of the center of the Mohr’s circle for
strain and R is the radius of that circle.
4. Procedure
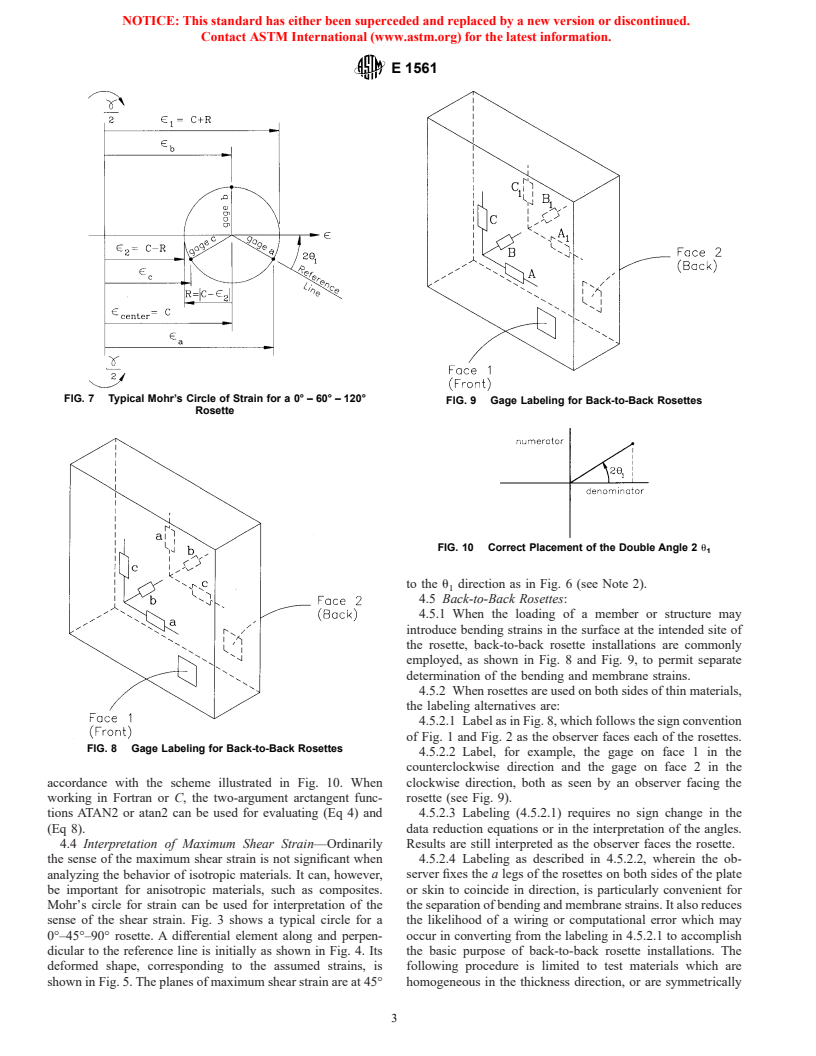
4.1 Fig. 3 shows a typical Mohr’s circle of strain for a
0° – 45° – 90° rosette. The calculations when e , e , e , are
a b c
given are:
e 1e
a c
C 5 (1)
FIG. 5 Deformed Shape of Differential Element
2 2
R 5 =~e 2 C! 1 ~e 2 C! (2)
a b
e 5 C 1 R (3)
e 5 C 2 R
g 5 2R
M
tan 2u 5 2 ~e 2 C! / e 2e (4)
1 b a c
4.1.1 If e b 1
reference line.
4.1.2 If e >C, then the e -axis is counterclockwise from the
b 1
reference line.
4.2 Fig. 7 shows a typical Mohr’s circle of strain for a
FIG. 6 Planes of Maximum Shear Strain
0° – 60° – 120° rosette. The calculations when e , e , e , are
a b c
e 5 C 1 R (7)
given are:
e 5 C 2 R
e 1e 1e
a b c
C 5 (5)
3 g 5 2R
M
2 2 2
~e 2e !
b c
R 5 =2 3@~e 2 C! 1 ~e 2 C! 1 ~e 2 C! # (6)
/ a b c
tan 2u 5 (8)
3~e 2 C!
=
a
4.2.1 If e − e < 0, then the e -axis is counterclockwise
c b 1
from the reference line.
4.2.2 If e − e = 0, then u = 0°.
c b 1
4.2.3 If e − e > 0, then the e -axis is clockwise from the
c b 1
reference line (see Note 1).
4.3 Identification of the Maximum Principal Strain Direc-
tion:
4.3.1 Care must be taken when determining the angle u
using (Eq 4) or (Eq 8) so that the calculated angle refers to the
direction of the maximum principal strain e rather than the
minimum principal strain e . Fig. 10 shows how the double
angle 2u can be placed in its correct orientation relative to the
reference line shown in Fig. 1 and Fig. 2. The terms “numera-
tor” and “denominator” refer to the numerator and denominator
of the right-hand sides of (Eq 4) and (Eq 8). When both
numerator and denominator are positive, as shown in Fig. 10,
the double angle 2u lies within the range 0° # 2u # 90°
1 1
counterclockwise of the reference line. Therefore, in this
particular case, the corresponding angle u lies within the range
0° # u # 45° counterclockwise of the reference line.
4.3.2 Several computer languages have arctangent functions
FIG. 3 Typical Mohr’s Circle of Strain for a 0° – 45° – 90°
Rosette that directly place the angle 2u in its correct orientation in
NOTICE: This standard has either been superceded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
E 1561
FIG. 7 Typical Mohr’s Circle of Strain for a 0° – 60° – 120°
FIG. 9
...