ASTM D4210-89(1996)e1
(Practice)Standard Practice for Intralaboratory Quality Control Procedures and a Discussion on Reporting Low-Level Data (Withdrawn 2002)
Standard Practice for Intralaboratory Quality Control Procedures and a Discussion on Reporting Low-Level Data (Withdrawn 2002)
SCOPE
1.1 This practice is applicable to all laboratories that provide chemical and physical measurements in water, and provides guidelines for intralaboratory control and suggested procedures for reporting low-level data.
1.2 The use of this practice is based on the assumptions that the analytical method used is appropriate for the task, is either essentially bias-free or the bias is known, is capable of being brought into a state of statistical control, and possesses adequate sensitivity to determine the analytes at the levels of interest.
1.3 Further, it is assumed that quality assurance procedures for field operations such as sample collection, container selection, preservation, transportation, and storage are proper.
1.4 This practice is also predicated upon the laboratory already having established a quality control system with development of an adequate reporting system such that the laboratory's performance can be substantiated.
General Information
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or
withdrawn. Contact ASTM International (www.astm.org) for the latest information.
e1
Designation: D 4210 – 89 (Reapproved 1996)
AMERICAN SOCIETY FOR TESTING AND MATERIALS
100 Barr Harbor Dr., West Conshohocken, PA 19428
Reprinted from the Annual Book of ASTM Standards. Copyright ASTM
Standard Practice for
Intralaboratory Quality Control Procedures and a
Discussion on Reporting Low-Level Data
This standard is issued under the fixed designation D 4210; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
e NOTE—Keywords were added editorially in May 1996.
1. Scope 3.1.4 in control—once a reliable estimate of the population
standard deviation is obtained, a deviation not exceeding 3s is
1.1 This practice is applicable to all laboratories that pro-
considered to be in control. Allowing deviations up to 3s imply
vide chemical and physical measurements in water, and pro-
an a(alpha) 5 0.0027 or about 3 chances in 1000 of judging an
vides guidelines for intralaboratory control and suggested
in control procedure to be out of control.
procedures for reporting low-level data.
3.1.5 limit of detection—a concentration of twice the crite-
1.2 The use of this practice is based on the assumptions that
rion of detection when it has been decided that the risk of
the analytical method used is appropriate for the task, is either
making a Type II error is to be equal to a Type I error (see
essentially bias-free or the bias is known, is capable of being
11.11).
brought into a state of statistical control, and possesses
3.1.6 Type I error, a(alpha) error—a statement that a
adequate sensitivity to determine the analytes at the levels of
substance is present when it is not.
interest.
3.1.7 Type II error, b(beta) error—a statement that a sub-
1.3 Further, it is assumed that quality assurance procedures
stance is not present (was not found) when the substance was
for field operations such as sample collection, container selec-
present.
tion, preservation, transportation, and storage are proper.
3.2 Definitions—For definitions of other terms used in this
1.4 This practice is also predicated upon the laboratory
practice, refer to Terminology D 1129.
already having established a quality control system with
development of an adequate reporting system such that the
4. Significance and Use
laboratory’s performance can be substantiated.
4.1 Any analytical procedure that is in statistical control will
have an inherent variability as one of its characteristics. For a
2. Referenced Documents
given procedure this variability is irreducible, that is, there is
2.1 ASTM Standards:
no identifiable factor or assignable cause that contributes to
D 1129 Terminology Relating to Water
procedure variation.
4.2 The measure of procedure variability for this practice is
3. Terminology
the estimate of the population standard deviation. The specific
3.1 Definitions of Terms Specific to This Standard:
population of interest can be either within an analytical set or
3.1.1 control charts—a charting of the variability of a
between set analyses or both.
procedure such that when some limit in variability is exceeded
4.3 In considering low level reporting the question is: is the
the method is deemed to be out of control.
substance present? This practice will aid in determining the
3.1.2 control limits—those upper and lower limits used to
risk taken in assigning that a substance is present, when it is
signal that a procedure is out of control.
not, and provide an assessment of criterion of detection.
3.1.3 criterion of detection—the minimum quantity (ana-
4.4 Procedure variability control limits are set by use of
lytical result) which must be observed before it can be stated
Shewhart control charts.
that a substance has been discerned with an acceptable prob-
5. Estimating Analytical Procedure Variability by
ability that the statement is true (see 11.11). The criterion of
Duplicate Analyses
detection must always be accompanied by the stated probabil-
ity.
5.1 For a crude estimate of population standard deviation,
initially conduct 5 or 6 duplicate analyses from samples of
nearly the same concentration. Accumulate additional data to
This practice is under the jurisdiction of ASTM Committee D-19 on Water and
obtain a reliable initial estimate of the population standard
is the responsibility of Subcommittee D19.02 on General Specifications, Technical
Resources, and Statistical Methods.
Current edition approved Jan. 27, 1989. Published March 1989. Originally
published as D 4210 – 83. Last previous edition D 4210 – 83. “Presentation of Data and Control Chart Analysis,” ASTM STP 15-D, ASTM,
Annual Book of ASTM Standards, Vol 11.01. 1976, pp. 93–103.
D 4210
2 2
deviation in which 40 to 50 data points (degrees of freedom)
5 n 2 1!s 1 n 2 1!s !/ n 1 n 2 2!#
@~~ ~ ~
1 1 2 2 1 2
are needed. They may be analyses of duplicate samples or
2 2 2
s 5 @~~60!s 1 ~40!s !/~60 1 40!#
1 2
standards determined either within analytical-set or between
sets depending on the information sought. However, with 2 2
5 @~60~1.796! 1 40~2.145! !/~60 1 40!#
highly labile constituents only within set analyses would be
s 5~193.537 1 184.041!/100
appropriate.
5.2 After performing the duplicate analyses, determine the
s 5 3.776
average difference between duplicates and divide this by 1.128
s 5 1.943 μg/L
to estimate the standard deviation. For an example of this
When a pooled estimate of the procedure standard deviation
calculation refer to Annex A1.
is obtained, new control limits should be calculated using the
5.3 Prepare necessary control charts as described in Section
revised estimate.
9.
6. Estimating Analytical Procedure Variability Using a 9. Setting Control Limits
Stable Standard
9.1 There are two goals in setting control limits. They
6.1 Using a stable standard in replicate for 50 or more data should be close enough to signal when there is trouble with a
points the procedure variability is estimated by calculating an
system, and they should be distant enough to discourage
estimate of the standard deviation in the usual way, tinkering with a system that is operating within its capabilities.
Since these two goals are in opposition, a compromise is
2 2
s 5 =~(x 2 nx¯ !/~n 2 1!
i
necessary. The compromise which has been found satisfactory
where:
in a great many applications is the use of 3s control limits, and
n they are illustrated here in 9.2. Warning control limits are
x¯ 5 x
(
i
described in 9.5.1.
n
i 5 1
9.2 Use of a Standard:
6.2 A discussion and illustration of the procedure is given in
9.2.1 Consider a sample whose concentration was prepared
Annex A2.
as 32.7 μg/L and is analyzed by a procedure whose estimated
6.3 Prepare a control chart with upper and lower limits as
standard deviation is 2.131 μg/L. The control limits are
described in Section 9.
therefore 32.7 6 3 3 2.131 or 26.31 and 39.09. Assuming that
7. Pooling Estimates to Improve Estimation of Standard
results can be read to tenths of a microgram, a result $26.3 and
Deviation
#39.1 is judged acceptable.
9.2.2 Typical Control Chart for Standards:
7.1 As additional data are obtained initial estimates of
Concentration
variability can be put on a sounder footing by pooling with
39.1______________________________ Upper control limit
estimates from the new information, assuming that no
32.7______________________________ Expected concentration
substantial change is apparent. To test for significant change in
26.3______________________________ Lower control limit
2 2
Time (Sequence)
variability the ratio of the two estimates s /s is calculated
1 2
and compared to appropriate values of the F distribution to test
9.3 Use of an Unknown Duplicate:
if pooling the estimates of variability is proper.
9.3.1 Suppose an unknown duplicate sample is analyzed in
7.2 A discussion on and illustration of how to determine if
separate runs by a procedure whose estimated standard
the estimates of analytical procedure variance had changed to
deviation is 1.537 μg/L. The control limit for the range of the
where they should not be combined is given in Annex A3.
two analyses is 1.537 3 3.686 or 5.67 (3.686 is the proper
7.3 If a procedure variability appears to have changed 2
factor for duplicate ranges). Assuming that results can be read
significantly, the procedure should be carefully reviewed to
to tenths of a microgram, an absolute difference between the
ascertain the cause.
duplicates (their range)# 5.7 is judged acceptable.
7.4 When it appears that the variability of an analytical
9.3.2 Typical Control Chart for Duplicate Analyses Ranges:
procedure has not changed, a pooled estimate of variability
Range
may be obtained.
5.7 μg/L______________________________ Control limit
0 μg/L_______________________________ 0
8. Pooling Estimates of Variability
Time (Sequence)
8.1 The pooling method consists of weighting the two
9.4 A Special Case, Use of Recovery Data:
variance estimates by the degrees of freedom of the respective
9.4.1 The use of recovery data from spiked samples for
data sets from which they were obtained, summing the
control purposes presents some special problems which are
weighted variance estimates, and dividing the sum by the sum
dealt with in Annex A4. Begin with the estimation of the
of the degrees of freedom associated with the two estimates.
variability associated with the determination of recoveries.
The quotient which results is the pooled variance estimate, s ,
9.4.2 If the spiking recovery demonstrates a bias, the control
from which the new, pooled estimate of the standard deviation,
limits must be centered about the estimate of the bias.
s, is obtained.
9.4.3 Suppose the calculated estimation of spike population
8.2 Using the data of A3.1
variation expressed as a standard deviation is found to be
2 2 2
0.1532 mg/L as illustrated in Annex A4, then control limits
s 5 @~~ df !s 1 df !s !/ df 1 df !
~ ~ #
1 1 2 2 1 2
would be 63 3 0.1532 or − 0.46 mg/L and + 0.46 mg/L.
D 4210
9.5 Warning Limits: single analysis when the substance is not present to illustrate
9.5.1 Some analysts prefer to use warning limits 2s, along Type I error and the inferences that might be drawn from a
with the typical 3s limits previously described. For 2s limits single analysis at two different actual concentrations to
the factors (f) to use times the standard deviation [(f)s] are illustrate Type II error. Of course inferences as to water quality
respectively (9.2), f 5 2; (9.3), f 5 2.834; (9.4), f 5 2. are seldom, if ever, based on the result of a single analysis. A
single result is used here to simplify the exposition.
10. Recommended Control Sample Frequency
11.4 If the standard deviation, s, of an analytical procedure
10.1 Until experience with the method dictates otherwise, to has been determined at low concentrations including 0, then
monitor accuracy, one quality control sample of expected value the probability of making a Type I error can be set by choosing
should be included with every ten analyses or with each batch, an appropriatea (alpha) level to determine the criterion of
whichever results in the greater frequency. detection (see 3.1.3).
10.2 To monitor precision, one quality control sample
11.5 For example, suppose that the standard deviation, s,of
should be included with every 10 analyses or with each batch an analytical procedure is 6 μg/L and that an a(alpha) of 0.05
of analyses run at the same time, whichever results in the
is deemed acceptable so that the probability of making a Type
greater frequency. If duplicates are used to monitor precision, I error is set at 5 %. The criterion of detection can then be
they should be analysed in different runs when a between run
found from a table of cumulative normal probabilities to be
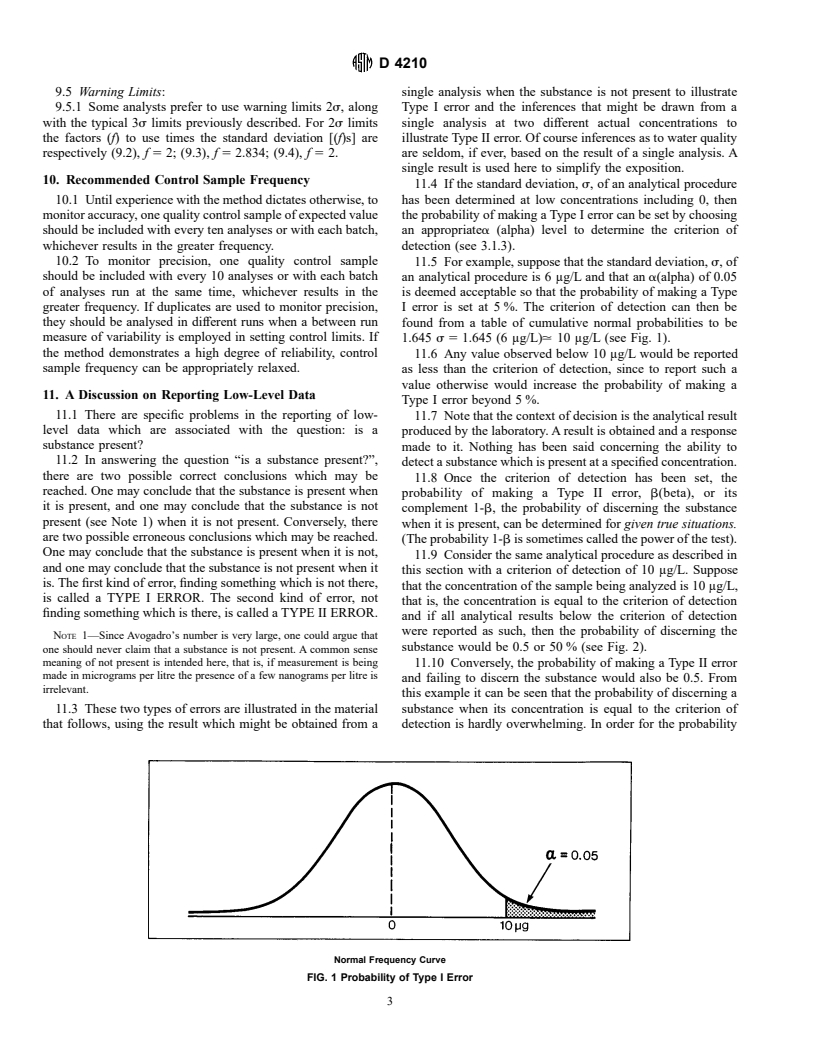
measure of variability is employed in setting control limits. If 1.645 s5 1.645 (6 μg/L). 10 μg/L (see Fig. 1).
the method demonstrates a high degree of reliability, control
11.6 Any value observed below 10 μg/L would be reported
sample frequency can be appropriately relaxed.
as less than the criterion of detection, since to report such a
value otherwise would increase the probability of making a
11. A Discussion on Reporting Low-Level Data
Type I error beyond 5 %.
11.1 There are specific problems in the reporting of low-
11.7 Note that the context of decision is the analytical result
level data which are associated with the question: is a
produced by the laboratory. A result is obtained and a response
substance present?
made to it. Nothing has been said concerning the ability to
11.2 In answering the question “is a substance present?”,
detect a substance which is present at a specified concentration.
there are two possible correct conclusions which may be
11.8 Once the criterion of detection has been set, the
reached. One may conclude that the substance is present when
probability of making a Type II error, b(beta), or its
it is present, and one may conclude that the substance is not
complement 1-b, the probability of discerning the substance
present (see Note 1) when it is not present. Conversely, there
when it is present, can be determined for given true situations.
are two possible erroneous conclusions which may be reached.
(The probability 1-b is sometimes called the power of the test).
One may conclude that the substance is present when it is not,
11.9 Consider the same analytical procedure as described in
and one may conclude that the substance is not present when it
this section with a criterion of detection of 10 μg/L. Suppose
is. The first kind of error, finding something which is not there,
that the concentration of the sample being analyzed is 10 μg/L,
is called a TYPE I ERROR. The second kind of error, not
that is, the concentration is equal to the criterion of detection
finding something which is there, is called a TYPE II ERROR.
and if all analytical results below the criterion of detection
were reported as such, then the probability of discerning the
NOTE 1—Since Avogadro’s number is very large, one could argue that
substance would be 0.5 or 50 % (see Fig. 2).
one should never claim that a substance is not present. A common sense
meaning of not present is intended here, that is, if measurement is being
11.10 Conversely, the probability of making a Type II error
made in micrograms per litre the presence of a few nanograms per litre is
and failing to discern the substance would also be 0.5. From
irrelevant.
this example it can be seen that the probability of discerning a
11.3 These two types of errors are illustrated in the material substance when its concentratio
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.