ASTM E693-01(2007)
(Practice)Standard Practice for Characterizing Neutron Exposures in Iron and Low Alloy Steels in Terms of Displacements Per Atom (DPA), E 706(ID)
Standard Practice for Characterizing Neutron Exposures in Iron and Low Alloy Steels in Terms of Displacements Per Atom (DPA), E 706(ID)
SCOPE
1.1 This practice describes a standard procedure for characterizing neutron irradiations of iron (and low alloy steels) in terms of the exposure index displacements per atom (dpa) for iron.
1.2 Although the general procedures of this practice apply to any material for which a displacement cross section d(E) is known (see Practice E 521), this practice is written specifically for iron.
1.3 It is assumed that the displacement cross section for iron is an adequate approximation for calculating displacements in steels that are mostly iron (95 to 100 %) in radiation fields for which secondary damage processes are not important.
1.4 Procedures analogous to this one can be formulated for calculating dpa in charged particle irradiations. (See Practice E 521.)
1.5 The application of this practice requires knowledge of the total neutron fluence and flux spectrum. Refer to Practice E 521 for determining these quantities.
1.6 The correlation of radiation effects data is beyond the scope of this practice.
This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation:E693–01(Reapproved2007)
Standard Practice for
Characterizing Neutron Exposures in Iron and Low Alloy
Steels in Terms of Displacements Per Atom (DPA),
E706(ID)
This standard is issued under the fixed designation E693; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope E521 Practice for Neutron Radiation Damage Simulation
by Charged-Particle Irradiation
1.1 This practice describes a standard procedure for charac-
E560 PracticeforExtrapolatingReactorVesselSurveillance
terizing neutron irradiations of iron (and low alloy steels) in
Dosimetry Results, E 706(IC)
terms of the exposure index displacements per atom (dpa) for
E821 Practice for Measurement of Mechanical Properties
iron.
During Charged-Particle Irradiation
1.2 Although the general procedures of this practice apply
E853 Practice for Analysis and Interpretation of Light-
toanymaterialforwhichadisplacementcrosssection s (E)is
d
Water Reactor Surveillance Results, E706(IA)
known (see Practice E521), this practice is written specifically
for iron.
3. Terminology
1.3 Itisassumedthatthedisplacementcrosssectionforiron
3.1 Definitions for terms used in this practice can be found
is an adequate approximation for calculating displacements in
in Terminology E170.
steels that are mostly iron (95 to 100%) in radiation fields for
which secondary damage processes are not important.
4. Significance and Use
1.4 Procedures analogous to this one can be formulated for
4.1 Apressure vessel surveillance program requires a meth-
calculating dpa in charged particle irradiations. (See Practice
odology for relating radiation-induced changes in materials
E521.)
exposed in accelerated surveillance locations to the condition
1.5 The application of this practice requires knowledge of
of the pressure vessel (see Practices E560 and E853). An
the total neutron fluence and flux spectrum. Refer to Practice
important consideration is that the irradiation exposures be
E521 for determining these quantities.
expressed in a unit that is physically related to the damage
1.6 The correlation of radiation effects data is beyond the
mechanisms.
scope of this practice.
4.2 Amajorsourceofneutronradiationdamageinmetalsis
1.7 This standard does not purport to address all of the
the displacement of atoms from their normal lattice sites.
safety concerns, if any, associated with its use. It is the
Hence,anappropriatedamageexposureindexisthenumberof
responsibility of the user of this standard to establish appro-
times, on the average, that an atom has been displaced during
priate safety and health practices and determine the applica-
an irradiation. This can be expressed as the total number of
bility of regulatory limitations prior to use.
displaced atoms per unit volume, per unit mass, or per atom of
2. Referenced Documents thematerial.Displacementsperatomisthemostcommonway
2 ofexpresssingthisquantity.Thenumberofdpaassociatedwith
2.1 ASTM Standards:
a particular irradiation depends on the amount of energy
E170 TerminologyRelatingtoRadiationMeasurementsand
deposited in the material by the neutrons, and hence, depends
Dosimetry
on the neutron spectrum. (For a more extended discussion, see
Practice E521.)
This practice is under the jurisdiction of ASTM Committee E10 on Nuclear 4.3 Nosimplecorrespondenceexistsingeneralbetweendpa
Technology and Applications and is the direct responsibility of Subcommittee
and a particular change in a material property. A reasonable
E10.05 on Nuclear Radiation Metrology.
starting point, however, for relative correlations of property
CurrenteditionapprovedJune1,2007.PublishedJuly2007.Originallyapproved
changes produced in different neutron spectra is the dpa value
in 1979. Last previous edition approved in 2001 as E693–01(2007). DOI:
10.1520/E0693-01R07.
associated with each environment. That is, the dpa values
For referenced ASTM standards, visit the ASTM website, www.astm.org, or
contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
Standards volume information, refer to the standard’s Document Summary page on Withdrawn. The last approved version of this historical standard is referenced
the ASTM website. on www.astm.org.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
E693–01 (2007)
themselves provide a spectrum-sensitive index that may be a a comparison of the previous edition (Practice E693-94) and
useful correlation parameter, or some function of the dpa currently recommended dpa estimates for several neutron
values may affect correlation. spectra.
4.4 Since dpa is a construct that depends on a model of the
5. Procedure
neutron interaction processes in the material lattice, as well as
the cross section (probability) for each of these processes, the
5.1 The displacement rate at time t is calculated as follows:
value of dpa would be different if improved models or cross
`
dpa/s 5 s E!f E,t!dE (1)
~ ~
sections are used. The calculated dpa cross section for ferritic * d
iron, as given in this practice, is determined by the procedure
where:
given in 6.3. A considerable body of irradiated materials data
s (E) = the displacement cross section for a particular
d
has been reported using dpa cross sections based on the iron
material, and
ENDF/B-IV (1, 2) cross section. The recent changes in the
f(E,t) dE = the fluence rate of neutrons in the energy
iron cross section (3), the recommendation to use the updated
interval E to E+ dE.
iron cross sections in radiation transport calculations of pres-
5.2 The exposure index, dpa, is then the time integrated
sure vessel spectra (4), and the recent availability of ENDF/
value of the displacement rate, calculated as follows:
B-VI iron dpa cross section calculations (1, 2, 5) have resulted
t `
r
in the update of the recommended dpa cross section to reflect
dpa 5 f ~t! s ~E!c~E,t!dEdt (2)
* *
tot d
0 0
the ENDF/B-VI cross sections (1). Although the ENDF/B-VI
based dpa cross section differs from the previously recom-
where:
mendedENDF/B-IVdpacrosssection (1)byabout60%inthe
f (t) = the time dependent fluence rate intensity, and
tot
energy region around 10 keV, by about 10% for energies
c(E,t) = the fluence rate spectrum normalized to give unit
between 100 keV and 2 MeV, and by a factor of 4 near 1 keV
integral fluence rate at any time when integrated
duetotheopeningofreactionchannelsinthecrosssection,the
over energy.
integral iron dpa values are much less sensitive to the change
5.2.1 If the fluence rate spectrum is constant over the
in cross sections.The update from ENDF/B-IVto ENDF/B-VI
duration, t , of the irradiation, then:
r
dpa rates when applied to the H. B. Robinson-2 pressurized
`
water reactor results in “up to ;4% higher dpa rates in the
dpa5f t s ~E!c~E!dE5f t s¯ (3)
tot r* d tot r d
region close to the pressure vessel outer surface” and in
where s¯ =the spectrum-average displacement cross sec-
d
“slightly lower dpa rates . close to the pressure vessel inner
tion.
wall”(6,7).Thustheupdateoftherecommendeddpaexposure
5.3 It is assumed for purposes of this practice that the
parameter to reflect an iron cross section consistent with that
fluence f t and the spectrum c(E) are known.
tot r
used in the current radiation transport calculations is “not
expected to introduce a bias in embrittlement data bases” (6)
6. Calculation
based on the change in the dpa cross section. Table 1 presents
6.1 The integral can be evaluated by a simple numerical
integration as follows:
N
`
s ~E!f~E!dE 5 ~s ! f DE (4)
* (
d d i i i
4 0 i 51
The boldface numbers in parentheses refer to the list of references appended to
this practice.
TABLE 1 Changes in Spectrum-Integrated dpa for Benchmark Neutron Spectra
A
Neutron Spectrum Spectrum-averaged dpa cross section (barns)
“Old” ENDF/B-IV-based “Current” ENDF/B-VI-based Difference ([Current - Old]/
E693 response E693 response Old) (%)
ENDF/B-VI U Thermal Fission (1, 2) 875.55 858.54 –1.9
Materials Dosimetry Reference Facility (MDRF) (8) 345.03 343.58 –0.42
CFRMF (9, 10) 382.94 387.08 1.08
Intermediate-energy Standard Neutron Field (ISNF) (10, 11) 483.63 480.00 –0.75
Arkansas Nuclear ONE-1 (ANO) Cavity (12, 13) 134.40 139.44 3.75
ORNL Poolside Facility (PSF) T/4 position (12, 14) 242.14 238.33 –1.57
Oak Ridge Research Reactor (ORR) (10) 291.68 288.86 –0.97
Yayoi (10) 613.12 609.03 –0.67
BIGTEN (10, 15) 334.98 341.25 1.87
H.B. Robinson-2, in the vessel wall, close to the inner surface (6, 7) 219.43 218.81 –0.28
H.B. Robinson-2, ; ⁄4 T vessel wall (6, 7) 245.17 249.24 1.66
H.B. Robinson-2, ; ⁄4 T vessel wall (6, 7) 203.68 211.23 3.71
A –10
The spectrum-average dpa values in this table were computed using Eq 11 in a 640 SAND-II energy group representation and a lower integration bound of E =10
o
MeV.
NOTE 1—Table 1 is included to illustrate the effect on the dpa cross sections resulting from the change from the ENDF/B-IV to ENDF/B-VI cross
sections. The spectrum-average cross section values given are not recommended for other uses because of their sensitivity to the assumed spectrum
representations and the lower energy integration limit.
E693–01 (2007)
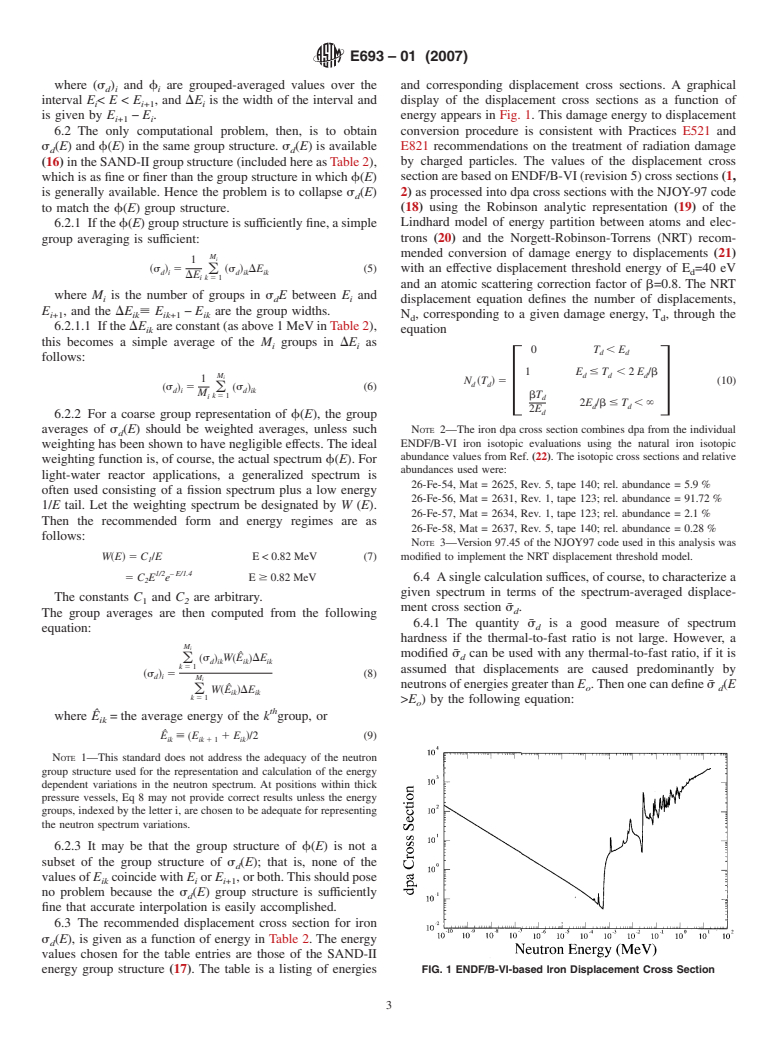
where (s ) and f are grouped-averaged values over the and corresponding displacement cross sections. A graphical
d i i
interval E< E < E , and DE is the width of the interval and display of the displacement cross sections as a function of
i i+1 i
is given by E − E. energy appears in Fig. 1. This damage energy to displacement
i+1 i
6.2 The only computational problem, then, is to obtain conversion procedure is consistent with Practices E521 and
E821 recommendations on the treatment of radiation damage
s (E) and f(E) in the same group structure. s (E) is available
d d
(16)intheSAND-IIgroupstructure(includedhereasTable2), by charged particles. The values of the displacement cross
sectionarebasedonENDF/B-VI(revision5)crosssections (1,
which is as fine or finer than the group structure in which f(E)
is generally available. Hence the problem is to collapse s (E) 2) as processed into dpa cross sections with the NJOY-97 code
d
(18) using the Robinson analytic representation (19) of the
to match the f(E) group structure.
6.2.1 Ifthe f(E)groupstructureissufficientlyfine,asimple Lindhard model of energy partition between atoms and elec-
trons (20) and the Norgett-Robinson-Torrens (NRT) recom-
group averaging is sufficient:
mended conversion of damage energy to displacements (21)
M
i
~s ! 5 ~s ! DE (5) with an effective displacement threshold energy of E =40 eV
(
d i d ik ik d
DE
i k 51
and an atomic scattering correction factor of b=0.8. The NRT
where M is the number of groups in s E between E and
i d i displacement equation defines the number of displacements,
E , and the DE [ E − E are the group widths.
i+1 ik ik+1 ik N , corresponding to a given damage energy, T , through the
d d
6.2.1.1 Ifthe DE areconstant(asabove1MeVinTable2),
ik equation
this becomes a simple average of the M groups in DE as
i i
0 T , E
d d
follows:
1 E # T ,2 E /b
M d d d
i
N ~T ! 5 (10)
d d
~s ! 5 ~s ! (6)
(
d i d ik
M
bT
i k 51
3 d 4
2E /b# T ,`
d d
2E
d
6.2.2 For a coarse group representation of f(E), the group
averages of s (E) should be weighted averages, unless such NOTE 2—The iron dpa cross section combines dpa from the individual
d
ENDF/B-VI iron isotopic evaluations using the natural iron isotopic
weighting has been shown to have negligible effects.The ideal
abundance values from Ref. (22). The isotopic cross sections and relative
weighting function is, of course, the actual spectrum f(E). For
abundances used were:
light-water reactor applications, a generalized spectrum is
26-Fe-54, Mat = 2625, Rev. 5, tape 140; rel. abundance = 5.9%
often used consisting of a fission spectrum plus a low energy
26-Fe-56, Mat = 2631, Rev. 1, tape 123; rel. abundance = 91.72%
1/E tail. Let the weighting spectrum be designated by W (E).
26-Fe-57, Mat = 2634, Rev. 1, tape 123; rel. abundance = 2.1%
Then the recommended form and energy regimes are as
26-Fe-58, Mat = 2637, Rev. 5, tape 140; rel. abundance = 0.28%
follows:
NOTE 3—Version 97.45 of the NJOY97 code used in this analysis was
W~E! 5 C /E E<0.82MeV (7) modified to implement the NRT displacement threshold model.
1/2 – E/1.4
5 C E e E$0.82MeV 6.4 Asinglecalculationsuffices,ofcourse,tocharacterizea
given spectrum in terms of the spectrum-averaged displace-
The constants C and C are arbitrary.
1 2
ment cross section s¯ .
d
The group averages are then computed from the following
6.4.1 The quantity s¯ is a good measure of spectrum
d
equation:
hardness if the thermal-to-fast ratio is not large. However, a
M
i
modified s¯ can be used with any thermal-to-fast ratio, if it is
d
~s ! W~Ê !DE
( d ik ik ik
k 51
assumed that displacements are caused predominantly by
~s ! 5 (8)
d i M
i
neutronsofenergiesgreaterthan E .Thenonecandefine s¯ (E
o d
W~Ê !DE
(
ik ik
k 51
>E ) by the following equation:
o
th
where Ê =the average energy of the k group, or
ik
Ê [ ~E 1 E !/2 (9)
ik ik 11 ik
NOTE 1—This standard does not address the adequacy of the neutron
group structure used for the representation and calculation of the energy
dependent variations in the neutron spectrum. At positions within thick
pressure vessels, Eq 8 may not provide correct results unless the energy
groups, indexed by the letter i, are chosen to be adequate for representing
the neutron spectrum variations.
6.2.3 It may be that the group structure of f(E) is not a
subset of the group structure of s (E); that is, none of the
d
valuesof E coincidewith E or E ,orboth.Thisshouldpose
ik i i+1
no problem because the s (E) group structure is sufficiently
d
fine that accurate interpolation is easily accomplished.
6.3 The recommended displacement cross section for iron
s (E), is given as a function of energy in Table 2. The energy
d
values chosen for the table entries are those of the SAND-II
energy group structure (17). The table is a listing of energies FIG. 1 ENDF/B-VI-based Iron Displacement Cross Section
E693–01 (2007)
`
dpa cross section is not available at present, although covari-
s ~E!f~E!dE
* d
E
o
ance matrices for the individual File 3 nuclear reaction cross
s ~E . E ! 5 (11)
d 0 `
sections which contribute to the dpa can be found in File 33 of
f~E! dE
*
E
o
the ENDF/B-VI cross section evaluations (1). For a discussion
and
of the effect of the energy dependence of s (E) on the relative
d
accuracy of the dpa calculation s
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.