ASTM E81-96(2001)
(Test Method)Standard Test Method for Preparing Quantitative Pole Figures
Standard Test Method for Preparing Quantitative Pole Figures
SCOPE
1.1 This test method covers the use of the X-ray diffractometer to prepare quantitative pole figures.
1.2 The test method consists of several experimental procedures. Some of the procedures (1-5) permit preparation of a complete pole figure. Others must be used in combination to produce a complete pole figure.
1.3 Pole figures (6) and inverse pole figures (7-10) are two-dimensional averages of the three-dimensional crystallite ori- entation distribution. Pole figures may be used to construct either inverse pole figures (11-13) or the crystallite orientation distribution (14-21). Development of series expansions of the crystallite orientation distribution from reflection pole figures (22, 23) makes it possible to obtain a series expansion of a complete pole figure from several incomplete pole figures. Pole figures or inverse pole figures derived by such methods shall be termed calculated. These techniques will not be described herein.
1.4 Provided the orientation is homogeneous through the thickness of the sheet, certain procedures (1-3) may be used to obtain a complete pole figure.
1.5 Provided the orientation has mirror symmetry with respect to planes perpendicular to the rolling, transverse, and normal directions, certain procedures (4, 5, 24) may be used to obtain a complete pole figure.
1.6 The test method emphasizes the Schulz reflection technique (25). Other techniques (3, 4, 5, 24) may be considered variants of the Schulz technique and are cited as options, but not described herein.
1.7 The test method also includes a description of the transmission technique of Decker, et al (26), which may be used in conjunction with the Schulz reflection technique to obtain a complete pole figure.
1.8 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E 81 – 96 (Reapproved 2001)
Standard Test Method for
Preparing Quantitative Pole Figures
ThisstandardisissuedunderthefixeddesignationE81;thenumberimmediatelyfollowingthedesignationindicatestheyearoforiginal
adoptionor,inthecaseofrevision,theyearoflastrevision.Anumberinparenthesesindicatestheyearoflastreapproval.Asuperscript
epsilon (e) indicates an editorial change since the last revision or reapproval.
1. Scope priate safety and health practices and determine the applica-
bility of regulatory limitations prior to use.
1.1 This test method covers the use of the X-ray diffracto-
meter to prepare quantitative pole figures.
2. Summary of Test Method
1.2 The test method consists of several experimental proce-
2 2.1 The test method consists of characterizing the distribu-
dures. Some of the procedures (1-5) permit preparation of a
tion of orientations of selected lattice planes with respect to
complete pole figure. Others must be used in combination to
sample-fixed coordinates (6). The distribution will usually be
produce a complete pole figure.
obtained by measurement of the intensity of X rays diffracted
1.3 Pole figures (6) and inverse pole figures (7-10) are two
by the sample. In such measurements the detector and associ-
dimensional averages of the three-dimensional crystallite ori-
ated limiting slits are fixed at twice the appropriate Bragg
entation distribution. Pole figures may be used to construct
angle,andthediffractedintensityisrecordedastheorientation
either inverse pole figures (11-13) or the crystallite orientation
of the sample is changed (1-6, 25, 26, 27).After the measured
distribution (14-21). Development of series expansions of the
data have been corrected, as necessary, for background, defo-
crystallite orientation distribution from reflection pole figures
cusing, and absorption, and normalized to have an average
(22, 23) makes it possible to obtain a series expansion of a
value of unity, the results may be plotted in stereographic or
completepolefigurefromseveralincompletepolefigures.Pole
equal-area projection.
figuresorinversepolefiguresderivedbysuchmethodsshallbe
2.2 The geometry of the Schulz (25) reflection method is
termed calculated. These techniques will not be described
illustrated in Fig. 1. Goniometers employing this geometry are
herein.
commercially available. The source of X rays is indicated by
1.4 Provided the orientation is homogeneous through the
L.SlitS1limitsdivergenceoftheincidentbeamintheplaneof
thickness of the sheet, certain procedures (1-3) may be used to
projection. Slit S2 limits divergence perpendicular to the plane
obtain a complete pole figure.
of projection. The sample, indicated by crosshatching, may be
1.5 Provided the orientation has mirror symmetry with
tilted about the axis FF8, which is perpendicular to the
respect to planes perpendicular to the rolling, transverse, and
diffractometer axis and lies in the plane of the sample. The tilt
normal directions, certain procedures (4, 5, 24) may be used to
angle was denoted f by Schulz (25). The sample position
obtain a complete pole figure.
shown in Fig. 1 corresponds to f=0 deg, for which approxi-
1.6 The test method emphasizes the Schulz reflection tech-
mateparafocusingconditionsexistatthedetectorslit,S3.With
nique (25). Other techniques (3, 4, 5, 24) may be considered
theapplicationofadefocusingcorrection,thismethodisuseful
variants of the Schulz technique and are cited as options, but
over a range of colatitude f from 0 deg to approximately 75
not described herein.
deg.
1.7 The test method also includes a description of the
2.2.1 Tilting the sample about FF8, so as to reduce the
transmission technique of Decker, et al (26), which may be
distance between L and points in the sample surface above the
used in conjunction with the Schulz reflection technique to
plane of projection, causes X rays diffracted from these points
obtain a complete pole figure.
to be displaced to the left of the center of S3, while X rays
1.8 This standard does not purport to address all of the
diffractedfrompointsinthesamplesurfacebelowtheplaneof
safety concerns, if any, associated with its use. It is the
projection are displaced to the right of the center of S3. The
responsibility of the user of this standard to establish appro-
displacement is equal to 2D tan f cos u, where D is the
distance above or below the plane of projection. The inte-
This test method is under the jurisdiction of ASTM Committee E04 on grated, or total, diffracted intensity is influenced only slightly
Metallography and is the direct responsibility of Subcommittee E04.11 on X-Ray
by tilting the sample (28). Insofar as possible, the detector slit
and Electron Metallography.
Current edition approved May 10, 1996. Published July 1996. Originally
published as E81–49T. Last previous edition E81–90.
2 3
Theboldfacenumbersinparenthesesrefertothelistofreferencesattheendof Available from Philips Electronics Instruments, Inc., 85 McKee Drive, Mah-
this test method. wah, NJ 07430, and Siemens Corp., 186 Wood Ave. So., Iselin, NJ 08830.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
E 81 – 96 (2001)
crystallite orientations in three dimensions. Data for construct-
ing pole figures are obtained with X-ray diffractometers, using
reflection and transmission techniques.
3.2 Several alternative procedures may be used. Some
produce complete pole figures. Others yield partial pole fig-
ures, which may be combined to produce a complete figure.
4. Apparatus
4.1 Source of X Rays—A beam of characteristic X rays of
substantially constant intensity is required. Characteristic Kal-
pha radiation of chromium, iron, cobalt, nickel, copper, mo-
lybdenum, and silver have all been used successfully, depend-
ing on the chemical composition of the specimen. Insofar as
possible, the radiation selected shall provide sufficient angular
FIG. 1 Geometry of Reflection Method.
dispersion to permit the resolution of peaks to be measured,
and shall not produce excessive fluorescence in the sample.
Linear absorption coefficients (29) for selected elements are
shallbeofsufficientwidthtoincludethedefocusedlineprofile
given in Table 2. Lower energy radiation (Cr, Fe, Co, Ni, Cu)
corresponding to the maximum sample tilt for which measure-
is generally preferred for reflection pole figure measurements
ments are to be made. Because of interferences from neigh-
as it provides greater angular dispersion. Higher energy radia-
boring diffraction peaks and physical limitations on sample
tion (Mo,Ag) is generally preferred for transmission measure-
size and detector slit width, it is necessary to limit vertical
divergence of the incident beam. A widely used pole figure ments.
4.2 Slits—Suitable slits shall be provided to limit horizon-
goniometer with a focal spot to the center of the sample
distanceof172mmemploysa0.5-mmslitlocated30mmfrom tal (in the plane of projection of Figs. 1 and 2) and vertical
(perpendicular to the plane of projection of Figs. 1 and 2)
the center of the sample for this purpose. Measured intensities
maybecorrectedfordefocusingbycomparisonwithintensities divergenceoftheincidentbeam.Horizontaldivergencesof1to
3 deg for reflection and 0.5 deg for transmission are typical.
diffractedbyarandomlyorientedspecimenofsimilarmaterial,
Vertical divergences of 0.2 deg for reflection and 1 deg for
or byemploying the theoretically calculated corrections (28).
transmission are typical. Insofar as possible, the receiving slit
2.3 The geometry of the transmission technique of Decker,
shall be of sufficient width to include the diffracted peak.
et al (26) is shown in Fig. 2. In contrast to the reflection
Receiving slits corresponding to 1 deg 2−theta are typical.
method, X rays diffracted from different points in the sample
4.3 Specimen Holder—Reflection Method:
diverge,makingtheresolutionofadjacentpeaksmoredifficult.
4.3.1 The specimen holder for the reflection method shall
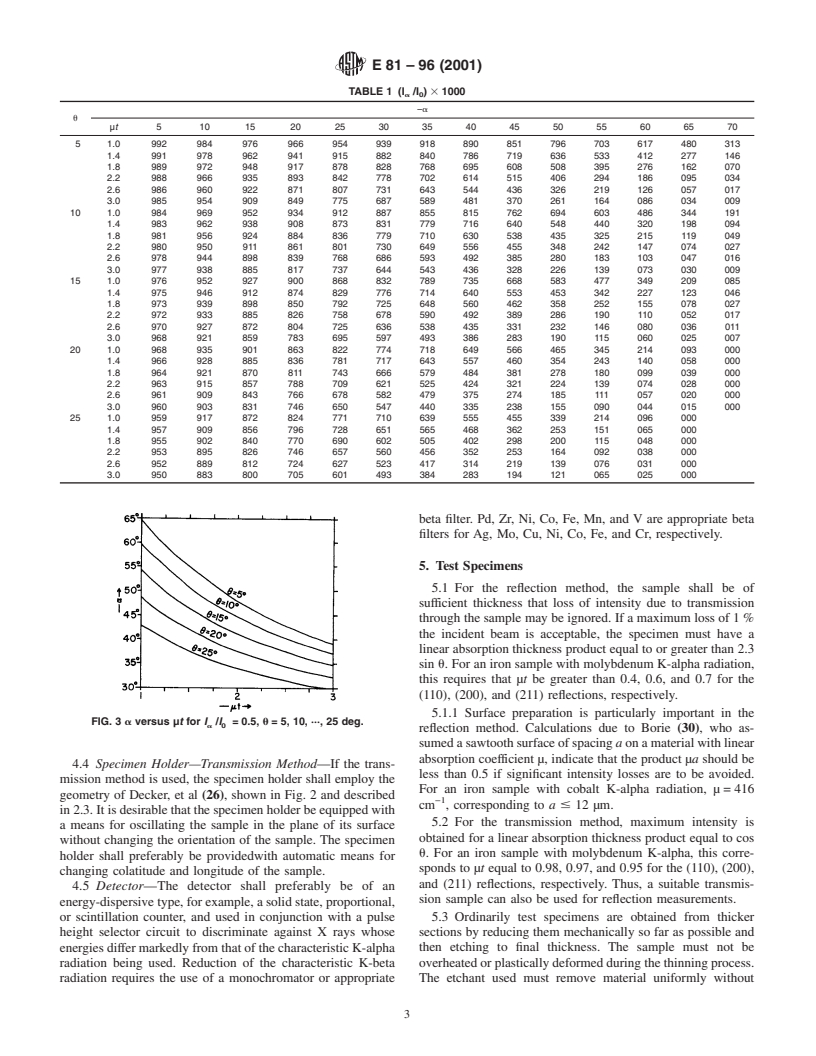
Theratioofthediffractedintensityat a=−5,−10,···,−70deg,
preferablyemploytheSchulzreflectiongeometryillustratedin
tothediffractedintensityat a=0deg,calculatedinaccordance
Fig. 1 and described in 2.2. It is desirable that the specimen
with the expression given by Decker, et al (26) for linear
holder be equipped with a means for oscillating the sample in
absorption thickness product, µt,=1.0, 1.4, ···, 3.0, and, for
the plane of its surface without changing the orientation of the
u=5, 10,··· , 25 deg is given in Table 1. These data may be
sample.Itisalsodesirablethatthemagnitudeoftheoscillation
used as a guide to determine the useful range of a for a given
be variable. The specimen holder shall preferably be provided
µtand u.If,forexample, I /I isrestrictedtovalues$0.5,one
a 0
with automatic means for changing colatitude and longitude of
arrives at the series of curves shown in Fig. 3.
the sample.
3. Significance and Use
4.3.2 Alternative reflection geometries include those of
Bakarian(1),FieldandMarchant(27),andJetterandBorie(2).
3.1 Pole figures are two-dimensional graphic representa-
The method of Bakarian requires machining a number of
tions, on polar coordinate paper, of the average distribution of
cylindrical specimens whose axes are perpendicular to the
sheet normal direction. Each specimen provides intensity data
alongoneparalleloflongitude.ThemethodofJetterandBorie
entails the preparation of a spherical specimen. In the methods
ofBakarianandofJetterandBorie,thesampleshall,insofaras
possible, be prepared from homogeneous material. These
methods have the advantage that intensity data need not be
corrected for absorption or defocusing. They do not permit
oscillation of the sample. Equipment is not currently commer-
cially available for these methods.
4.3.3 The method of Field and Marchant (27) requires an
absorption correction. If this method is used in conjunction
with the transmission method of Decker, et al (26),itis
necessarytouseeitherdifferentordersofreflectionordifferent
FIG. 2 Geometry of Transmission Method. radiations in order to obtain a complete pole figure.
E 81 – 96 (2001)
TABLE 1 (I /I ) 3 1000
a 0
−a
u
µt 5 10 15 20 25303540455055606570
5 1.0 992 984 976 966 954 939 918 890 851 796 703 617 480 313
1.4 991 978 962 941 915 882 840 786 719 636 533 412 277 146
1.8 989 972 948 917 878 828 768 695 608 508 395 276 162 070
2.2 988 966 935 893 842 778 702 614 515 406 294 186 095 034
2.6 986 960 922 871 807 731 643 544 436 326 219 126 057 017
3.0 985 954 909 849 775 687 589 481 370 261 164 086 034 009
10 1.0 984 969 952 934 912 887 855 815 762 694 603 486 344 191
1.4 983 962 938 908 873 831 779 716 640 548 440 320 198 094
1.8 981 956 924 884 836 779 710 630 538 435 325 215 119 049
2.2 980 950 911 861 801 730 649 556 455 348 242 147 074 027
2.6 978 944 898 839 768 686 593 492 385 280 183 103 047 016
3.0 977 938 885 817 737 644 543 436 328 226 139 073 030 009
15 1.0 976 952 927 900 868 832 789 735 668 583 477 349 209 085
1.4 975 946 912 874 829 776 714 640 553 453 342 227 123 046
1.8 973 939 898 850 792 725 648 560 462 358 252 155 078 027
2.2 972 933 885 826 758 678 590 492 389 286 190 110 052 017
2.6 970 927 872 804 725 636 538 435 331 232 146 080 036 011
3.0 968 921 859 783 695 597 493 386 283 190 115 060 025 007
20 1.0 968 935 901 863 822 774 718 649 566 465 345 214 093 000
1.4 966 928 885 836 781 717 643 557 460 354 243 140 058 000
1.8 964 921 870 811 743 666 579 484 381 278 180 099 039 000
2.2 963 915 857 788 709 621 525 424 321 224 139 074 028 000
2.6 961 909 843 766 678 582 479 375 274 185 111 057 020 000
3.0 960 903 831 746 650 547 440 335 238 155 090 044 015 000
25 1.0 959 917 872 824 771 710 639 555 455 339 214 096 000
1.4 957 909 856 796 728 651 565 468 362 253 151 065 000
1.8 955 902 840 770 690 602 505 402 298 200 115 048 000
2.2 953 895 826 746 657 560 456 352 253 164 092 038 000
2.6 952 889 812 724 627 523 417 314 219 139 076 031 000
3.0 950 883 800 705 601 493 384 283 194 121 065 025 000
beta filter. Pd, Zr, Ni, Co, Fe, Mn, and V are appropriate beta
filters for Ag, Mo, Cu, Ni, Co, Fe, and Cr, respectively.
5. Test Specimens
5.1 For the reflection method, the sample shall be of
sufficient thickness that loss of intensity due to transmission
through the sample may be ignored. If a maximum loss of 1%
the incident beam is acceptable, the specimen must have a
linear absorption thickness product equal to or greater than 2.3
sin u. For an iron sample with molybdenum K-alpha radiation,
this requires that µt be greater than 0.4, 0.6, and 0.7 for the
(110), (200), and (211) reflections, respectively.
5.1.1 Surface preparation is particularly important in the
FIG. 3 a versus µt for I /I = 0.5, u = 5, 10, ···, 25 deg.
a 0
reflection method. Calculations due to Borie (30), who as-
sumedasawtoothsurfaceofspacing aonamaterialwithlinear
absorption coefficient µ, indicate that the product µa should be
4.4 Specimen Holder—Transmission Method—If the trans-
less than 0.5 if significant intensity losses are to be avoided.
mission method is used, the specimen holder shall employ the
For an iron sample with cobalt K-alpha radiation, µ=416
geometry of Decker, et al (26), shown in Fig. 2 and described
−1
cm , corresponding to a# 12 µm.
in2.3.Itisdesirablethatthespecimenholderbeequippedwith
5.2 For the transmission method, maximum intensity is
a means for oscillating the sample in the plane of its surface
obtained for a linear absorption thickness product equal to cos
without changing the orientation of the sample. The specimen
u. For an iron sample with molybdenum K-alpha, this corre-
holder shall preferably be providedwith automatic means for
sponds to µt equal to 0.98, 0.97, and 0.95 for the (110), (200),
changing colatitude and longitude of the sample.
and (211) reflections, respectively. Thus, a suitable transmis-
4.5 Detector—The detector shall preferably be of an
sion sample can also be used for reflection measurements.
energy-dispersivetype,forexample,asolidstate,proportional,
or scintillation counter, and used in conjunction with a pulse 5.3 Ordinarily test specimens are obtained from thicker
height selector circuit to discriminate against X rays whose sections by reducing them mechanically so far as possible and
energiesdiffermarkedlyfromthatofthecharacteristicK-alpha then etching to final thickness. The sample must not be
radiation being used. Reduction of the characteristic K-beta overheatedorplasticallydeformedduringthethinningprocess.
radiation requires the use of a monochromator or appropriate The etchant used must remove material uniformly without
E 81 – 96 (2001)
−1
TABLE 2 Linear Absorption Coefficient µ (cm ) for Selected Wavelengths and Elements
K-alpha Radi
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.