ASTM G172-03(2010)
(Guide)Standard Guide for Statistical Analysis of Accelerated Service Life Data
Standard Guide for Statistical Analysis of Accelerated Service Life Data
SIGNIFICANCE AND USE
The nature of accelerated service life estimation normally requires that stresses higher than those experienced during service conditions are applied to the material being evaluated. For non-constant use stress, such as experienced by time varying weather outdoors, it may in fact be useful to choose an accelerated stress fixed at a level slightly lower than (say 90 % of) the maximum experienced outdoors. By controlling all variables other than the one used for accelerating degradation, one may model the expected effect of that variable at normal, or usage conditions. If laboratory accelerated test devices are used, it is essential to provide precise control of the variables used in order to obtain useful information for service life prediction. It is assumed that the same failure mechanism operating at the higher stress is also the life determining mechanism at the usage stress. It must be noted that the validity of this assumption is crucial to the validity of the final estimate.
Accelerated service life test data often show different distribution shapes than many other types of data. This is due to the effects of measurement error (typically normally distributed), combined with those unique effects which skew service life data towards early failure time (infant mortality failures) or late failure times (aging or wear-out failures). Applications of the principles in this guide can be helpful in allowing investigators to interpret such data.
The choice and use of a particular acceleration model and life distribution model should be based primarily on how well it fits the data and whether it leads to reasonable projections when extrapolating beyond the range of data. Further justification for selecting models should be based on theoretical considerations.
Note 2—Accelerated service life or reliability data analysis packages are becoming more readily available in common computer software packages. This makes data reduction and analyses more directly accessible ...
SCOPE
1.1 This guide briefly presents some generally accepted methods of statistical analyses that are useful in the interpretation of accelerated service life data. It is intended to produce a common terminology as well as developing a common methodology and quantitative expressions relating to service life estimation.
1.2 This guide covers the application of the Arrhenius equation to service life data. It serves as a general model for determining rates at usage conditions, such as temperature. It serves as a general guide for determining service life distribution at usage condition. It also covers applications where more than one variable act simultaneously to affect the service life. For the purposes of this guide, the acceleration model used for multiple stress variables is the Eyring Model. This model was derived from the fundamental laws of thermodynamics and has been shown to be useful for modeling some two variable accelerated service life data. It can be extended to more than two variables.
1.3 Only those statistical methods that have found wide acceptance in service life data analyses have been considered in this guide.
1.4 The Weibull life distribution is emphasized in this guide and example calculations of situations commonly encountered in analysis of service life data are covered in detail. It is the intention of this guide that it be used in conjunction with Guide G166.
1.5 The accuracy of the model becomes more critical as the number of variables increases and/or the extent of extrapolation from the accelerated stress levels to the usage level increases. The models and methodology used in this guide are shown for the purpose of data analysis techniques only. The fundamental requirements of proper variable selection and measurement must still be met for a meaningful model to result.
General Information
Relations
Buy Standard
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: G172 − 03 (Reapproved2010)
Standard Guide for
Statistical Analysis of Accelerated Service Life Data
This standard is issued under the fixed designation G172; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope 2. Referenced Documents
1.1 This guide briefly presents some generally accepted 2.1 ASTM Standards:
G166Guide for Statistical Analysis of Service Life Data
methods of statistical analyses that are useful in the interpre-
G169Guide for Application of Basic Statistical Methods to
tation of accelerated service life data. It is intended to produce
Weathering Tests
a common terminology as well as developing a common
methodology and quantitative expressions relating to service
3. Terminology
life estimation.
3.1 Terms Commonly Used in Service Life Estimation:
1.2 This guide covers the application of the Arrhenius
3.1.1 acceleratedstress,n—thatexperimentalvariable,such
equation to service life data. It serves as a general model for
as temperature, which is applied to the test material at levels
determining rates at usage conditions, such as temperature. It
higher than encountered in normal use.
serves as a general guide for determining service life distribu-
3.1.2 beginning of life, n—this is usually determined to be
tion at usage condition. It also covers applications where more
the time of delivery to the end user or installation into field
than one variable act simultaneously to affect the service life.
service. Exceptions may include time of manufacture, time of
For the purposes of this guide, the acceleration model used for
repair, or other agreed upon time.
multiple stress variables is the Eyring Model. This model was
derivedfromthefundamentallawsofthermodynamicsandhas
3.1.3 cdf, n—the cumulative distribution function (cdf),
been shown to be useful for modeling some two variable
denoted by F(t), represents the probability of failure (or the
accelerated service life data. It can be extended to more than
population fraction failing) by time = (t). See 3.1.7.
two variables.
3.1.4 completedata,n—acompletedatasetisonewhereall
1.3 Only those statistical methods that have found wide of the specimens placed on test fail by the end of the allocated
acceptance in service life data analyses have been considered
test time.
in this guide.
3.1.5 endoflife,n—occasionallythisissimpleandobvious,
such as the breaking of a chain or burning out of a light bulb
1.4 TheWeibulllifedistributionisemphasizedinthisguide
filament. In other instances, the end of life may not be so
and example calculations of situations commonly encountered
catastrophic or obvious. Examples may include fading,
in analysis of service life data are covered in detail. It is the
yellowing, cracking, crazing, etc. Such cases need quantitative
intentionofthisguidethatitbeusedinconjunctionwithGuide
measurements and agreement between evaluator and user as to
G166.
the precise definition of failure. For example, when some
1.5 The accuracy of the model becomes more critical as the
critical physical parameter (such as yellowing) reaches a
number of variables increases and/or the extent of extrapola-
pre-defined level. It is also possible to model more than one
tion from the accelerated stress levels to the usage level
failure mode for the same specimen (that is, the time to reach
increases. The models and methodology used in this guide are
a specified level of yellowing may be measured on the same
shown for the purpose of data analysis techniques only. The
specimen that is also tested for cracking).
fundamental requirements of proper variable selection and
3.1.6 f(t), n—the probability density function (pdf), equals
measurement must still be met for a meaningful model to
the probability of failure between any two points of time t
result. (1)
dF t
~ !
and t ; f~t!5 . For the normal distribution, the pdf is the
(2)
dt
“bell shape” curve.
This guide is under the jurisdiction of ASTM Committee G03 on Weathering
and Durability and is the direct responsibility of Subcommittee G03.08 on Service
Life Prediction. For referenced ASTM standards, visit the ASTM website, www.astm.org, or
CurrenteditionapprovedJuly1,2010.PublishedJuly2010.Originallyapproved contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
in 2002. Last previous edition approved in 2002 as G172-03. DOI: 10.1520/ Standards volume information, refer to the standard’s Document Summary page on
G0172-03R10. the ASTM website.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
G172 − 03 (2010)
3.1.7 F(t),n—theprobabilitythatarandomunitdrawnfrom where:
the population will fail by time (t). Also F(t) = the decimal
F(t) = probability of failure by time (t) as defined in 3.1.7,
fraction of units in the population that will fail by time (t).The
t = units of time used for service life,
decimal fraction multiplied by 100 is numerically equal to the c = scale parameter, and
percent failure by time (t). b = shape parameter.
3.1.8 incomplete data, n—an incomplete data set is one
3.1.12.1 Discussion—The shape parameter (b), 3.1.12,isso
where (1) there are some specimens that are still surviving at
called because this parameter determines the overall shape of
the expiration of the allowed test time, or (2) where one or
the curve. Examples of the effect of this parameter on the
more specimens is removed from the test prior to expiration of
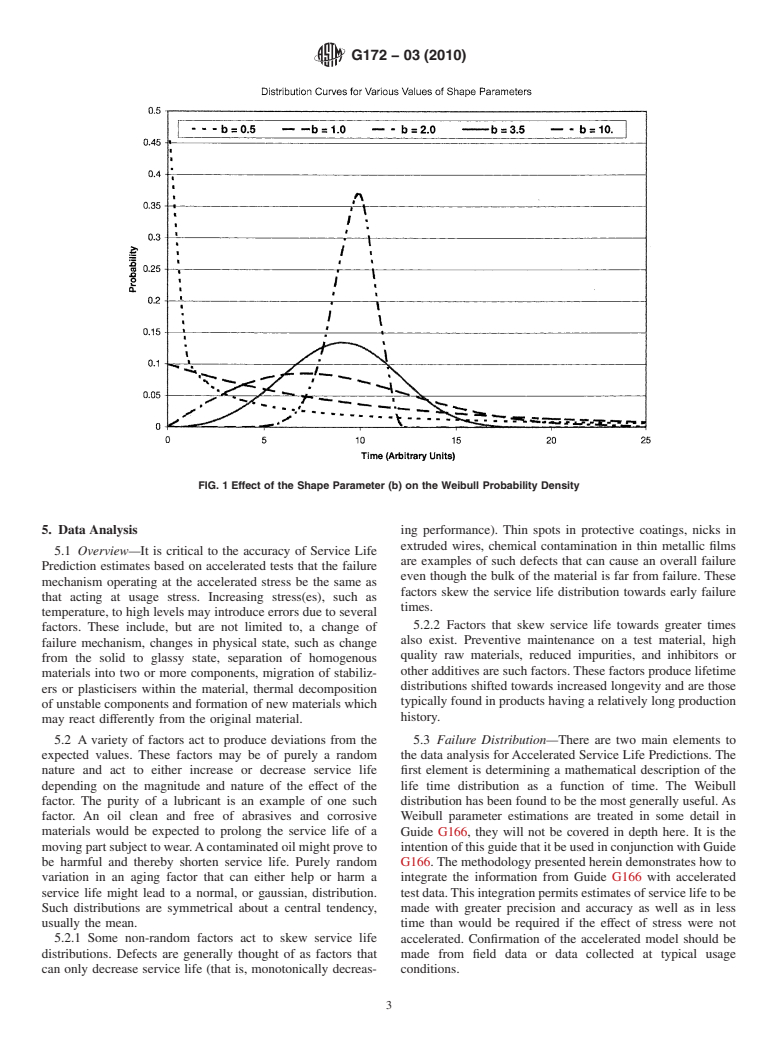
distribution curve are shown in Fig. 1.
the allocated test time. The shape and scale parameters of the
3.1.12.2 Discussion—The scale parameter (c), 3.1.12,isso
above distributions may be estimated even if some of the test
called because it positions the distribution along the scale of
specimensdidnotfail.Therearethreedistinctcaseswherethis
the time axis. It is equal to the time for 63.2% failure.
might occur.
NOTE 1—This is arrived at by allowing t to equal c in Eq 1. This then
3.1.8.1 multiple censored, n—specimens that were removed
-1
reduces to Failure Probability=1− e . which further reduces to equal 1
prior to the end of the test without failing are referred to as left
− 0.368 or 0.632.
censored or type II censored. Examples would include speci-
mens that were lost, dropped, mishandled, damaged or broken
4. Significance and Use
duetostressesnotpartofthetest.Adjustmentsoffailureorder
4.1 The nature of accelerated service life estimation nor-
can be made for those specimens actually failed.
mally requires that stresses higher than those experienced
3.1.8.2 specimen censored, n—specimens that were still
during service conditions are applied to the material being
surviving when the test was terminated after a set number of
evaluated. For non-constant use stress, such as experienced by
failures are considered to be specimen censored. This is
time varying weather outdoors, it may in fact be useful to
another case of right censored or type I censoring. See 3.1.8.3.
choose an accelerated stress fixed at a level slightly lower than
3.1.8.3 time censored, n—specimens that were still surviv- (say 90% of) the maximum experienced outdoors. By control-
ling all variables other than the one used for accelerating
ing when the test was terminated after elapse of a set time are
considered to be time censored. Examples would include degradation,onemaymodeltheexpectedeffectofthatvariable
at normal, or usage conditions. If laboratory accelerated test
experiments where exposures are conducted for a predeter-
mined length of time.At the end of the predetermined time, all devicesareused,itisessentialtoprovideprecisecontrolofthe
variables used in order to obtain useful information for service
specimens are removed from the test. Those that are still
surviving are said to be censored. This is also referred to as life prediction. It is assumed that the same failure mechanism
operating at the higher stress is also the life determining
rightcensoredortypeIcensoring.Graphicalsolutionscanstill
be used for parameter estimation.Aminimum of ten observed mechanismattheusagestress.Itmustbenotedthatthevalidity
ofthisassumptioniscrucialtothevalidityofthefinalestimate.
failuresshouldbeusedforestimatingparameters(thatis,slope
and intercept, shape and scale, etc.).
4.2 Accelerated service life test data often show different
3.1.9 material property, n—customarily, service life is con- distribution shapes than many other types of data. This is due
sidered to be the period of time during which a system meets
to the effects of measurement error (typically normally
critical specifications. Correct measurements are essential to distributed), combined with those unique effects which skew
produce meaningful and accurate service life estimates.
service life data towards early failure time (infant mortality
3.1.9.1 Discussion—There exists many ASTM recognized failures) or late failure times (aging or wear-out failures).
and standardized measurement procedures for determining
Applications of the principles in this guide can be helpful in
material properties. These practices have been developed allowing investigators to interpret such data.
within committees having appropriate expertise, therefore, no
4.3 The choice and use of a particular acceleration model
further elaboration will be provided.
and life distribution model should be based primarily on how
3.1.10 R(t), n—the probability that a random unit drawn
well it fits the data and whether it leads to reasonable
fromthepopulationwillsurviveatleastuntiltime(t).AlsoR(t)
projections when extrapolating beyond the range of data.
=thefractionofunitsinthepopulationthatwillsurviveatleast
Further justification for selecting models should be based on
until time (t); R(t)=1− F(t).
theoretical considerations.
NOTE 2—Accelerated service life or reliability data analysis packages
3.1.11 usage stress, n—the level of the experimental vari-
are becoming more readily available in common computer software
able that is considered to represent the stress occurring in
packages.Thismakesdatareductionandanalysesmoredirectlyaccessible
normal use. This value must be determined quantitatively for
to a growing number of investigators.This is not necessarily a good thing
accurate estimates to be made. In actual practice, usage stress
as the ability to perform the mathematical calculation, without the
may be highly variable, such as those encountered in outdoor fundamental understanding of the mechanics may produce some serious
errors. See Ref (1).
environments.
3.1.12 Weibull distribution, n—for the purposes of this
guide, the Weibull distribution is represented by the equation:
Theboldfacenumbersinparenthesesrefertothelistofreferencesattheendof
t b
S D
F t 51 2 e c (1) this standard.
~ !
G172 − 03 (2010)
FIG. 1 Effect of the Shape Parameter (b) on the Weibull Probability Density
5. Data Analysis ing performance). Thin spots in protective coatings, nicks in
extruded wires, chemical contamination in thin metallic films
5.1 Overview—It is critical to the accuracy of Service Life
are examples of such defects that can cause an overall failure
Prediction estimates based on accelerated tests that the failure
even though the bulk of the material is far from failure. These
mechanism operating at the accelerated stress be the same as
factors skew the service life distribution towards early failure
that acting at usage stress. Increasing stress(es), such as
times.
temperature, to high levels may introduce errors due to several
5.2.2 Factors that skew service life towards greater times
factors. These include, but are not limited to, a change of
also exist. Preventive maintenance on a test material, high
failure mechanism, changes in physical state, such as change
quality raw materials, reduced impurities, and inhibitors or
from the solid to glassy state, separation of homogenous
other additives are such factors.These factors produce lifetime
materials into two or more components, migration of stabiliz-
distributions shifted towards increased longevity and are those
ers or plasticisers within the material, thermal decomposition
typically found in products having a relatively long production
of unstable components and formation of new materials which
history.
may react differently from the original material.
5.2 A variety of factors act to produce deviations from the 5.3 Failure Distribution—There are two main elements to
expected values. These factors may be of purely a random the data analysis forAccelerated Service Life Predictions. The
nature and act to either increase or decrease service life first element is determining a mathematical description of the
depending on the magnitude and nature of the effect of the life time distribution as a function of time. The Weibull
factor. The purity of a lubricant is an example of one such distribution has been found to be the most generally useful.As
factor. An oil clean and free of abrasives and corrosive Weibull parameter estimations are treated in some detail in
materials would be expected to prolong the service life of a Guide G166, they will not be covered in depth here. It is the
movingpartsubjecttowear.Acontaminatedoilmightproveto intentionofthisguidethatitbeusedinconjunctionwithGuide
be harmful and thereby shorten service life. Purely random G166.Themethodologypresentedhereindemonstrateshowto
variation in an aging factor that can either help or harm a integrate the information from Guide G166 with accelerated
service life might lead to a normal, or gaussian, distribution. testdata.Thisintegrationpermitsestimatesofservicelifetobe
Such distributions are symmetrical about a central tendency, made with greater precision and accuracy as well as in less
usually the mean. time than would be required if the effect of stress were not
5.2.1 Some non-random factors act to skew service life accelerated. Confirmation of the accelerated model should be
distributions. Defects are generally thought of as factors that made from field data or data collected at typical usage
can only decrease service life (that is, monotonically decreas- conditions.
G172 − 03 (2010)
5.3.1 Establishing, in an accelerated time frame, a descrip- 5.4.5 The time element used in the Eq 3 is arbitrary. It can
tion of the distribution of frequency (or probability) of failure be the time for the first 5% failure, time for average failure,
time for 63.2% failure, time for 95% failure or any other
versus time in service is the objective o
...
This document is not anASTM standard and is intended only to provide the user of anASTM standard an indication of what changes have been made to the previous version. Because
it may not be technically possible to adequately depict all changes accurately, ASTM recommends that users consult prior editions as appropriate. In all cases only the current version
of the standard as published by ASTM is to be considered the official document.
Designation:G172–03 Designation: G172 – 03 (Reapproved 2010)
Standard Guide for
Statistical Analysis of Accelerated Service Life Data
This standard is issued under the fixed designation G172; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope
1.1 This guide briefly presents some generally accepted methods of statistical analyses that are useful in the interpretation of
accelerated service life data. It is intended to produce a common terminology as well as developing a common methodology and
quantitative expressions relating to service life estimation.
1.2 ThisguidecoverstheapplicationoftheArrheniusequationtoservicelifedata.Itservesasageneralmodelfordetermining
rates at usage conditions, such as temperature. It serves as a general guide for determining service life distribution at usage
condition. It also covers applications where more than one variable act simultaneously to affect the service life. For the purposes
of this guide, the acceleration model used for multiple stress variables is the Eyring Model. This model was derived from the
fundamental laws of thermodynamics and has been shown to be useful for modeling some two variable accelerated service life
data. It can be extended to more than two variables.
1.3 Only those statistical methods that have found wide acceptance in service life data analyses have been considered in this
guide.
1.4 The Weibull life distribution is emphasized in this guide and example calculations of situations commonly encountered in
analysis of service life data are covered in detail. It is the intention of this guide that it be used in conjunction with Guide G166.
1.5 The accuracy of the model becomes more critical as the number of variables increases and/or the extent of extrapolation
from the accelerated stress levels to the usage level increases. The models and methodology used in this guide are shown for the
purpose of data analysis techniques only. The fundamental requirements of proper variable selection and measurement must still
be met for a meaningful model to result.
2. Referenced Documents
2.1 ASTM Standards:
G166 Guide for Statistical Analysis of Service Life Data
G169 Guide for Application of Basic Statistical Methods to Weathering Tests
3. Terminology
3.1 Terms Commonly Used in Service Life Estimation:
3.1.1 accelerated stressaccelerated stress, n—that experimental variable, such as temperature, which is applied to the test
material at levels higher than encountered in normal use.
3.1.2 beginning of lifebeginning of life, n—this is usually determined to be the time of delivery to the end user or installation
into field service. Exceptions may include time of manufacture, time of repair, or other agreed upon time.
3.1.3 cdfcdf, n—the cumulative distribution function (cdf), denoted by F (t ), represents the probability of failure (or the
population fraction failing) by time = (t). See 3.1.7.
3.1.4 complete datacomplete data, n—a complete data set is one where all of the specimens placed on test fail by the end of
the allocated test time.
3.1.5 end of lifeend of life, n—occasionally this is simple and obvious, such as the breaking of a chain or burning out of a light
bulb filament. In other instances, the end of life may not be so catastrophic or obvious. Examples may include fading, yellowing,
cracking, crazing, etc. Such cases need quantitative measurements and agreement between evaluator and user as to the precise
definitionoffailure.Forexample,whensomecriticalphysicalparameter(suchasyellowing)reachesapre-definedlevel.Itisalso
possible to model more than one failure mode for the same specimen (that is, the time to reach a specified level of yellowing may
This guide is under the jurisdiction of ASTM Committee G03 on Weathering and Durability and is the direct responsibility of Subcommittee G03.08 on Service Life
Prediction.
Current edition approved Jan. 10, 2003. Published February 2003. DOI: 10.1520/G0172-03.
Current edition approved July 1, 2010. Published July 2010. Originally approved in 2002. Last previous edition approved in 2002 as G172-03. DOI:
10.1520/G0172-03R10.
ForreferencedASTMstandards,visittheASTMwebsite,www.astm.org,orcontactASTMCustomerServiceatservice@astm.org.ForAnnualBookofASTMStandards
volume information, refer to the standard’s Document Summary page on the ASTM website.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
G172 – 03 (2010)
be measured on the same specimen that is also tested for cracking).
3.1.6 f(t)f(t), n—the probability density function (pdf), equals the probability of failure between any two points of time t and
(1)
t ;f (t)= dF t! dt . For the normal distribution, the pdf is the “bell shape” curve.
~
(2)
/
3.1.7 F(t)F(t), n—the probability that a random unit drawn from the population will fail by time (t).Also F ( t) = the decimal
fraction of units in the population that will fail by time (t). The decimal fraction multiplied by 100 is numerically equal to the
percent failure by time (t).
3.1.8 incomplete dataincomplete data, n—an incomplete data set is one where (1) there are some specimens that are still
survivingattheexpirationoftheallowedtesttime,or(2)whereoneormorespecimensisremovedfromthetestpriortoexpiration
of the allocated test time. The shape and scale parameters of the above distributions may be estimated even if some of the test
specimens did not fail. There are three distinct cases where this might occur.
3.1.8.1 multiple censoredmultiple censored, n—specimens that were removed prior to the end of the test without failing are
referred to as left censored or type II censored. Examples would include specimens that were lost, dropped, mishandled, damaged
or broken due to stresses not part of the test. Adjustments of failure order can be made for those specimens actually failed.
3.1.8.2 specimen censoredspecimen censored, n—specimens that were still surviving when the test was terminated after a set
number of failures are considered to be specimen censored.This is another case of right censored or type I censoring. See 3.1.8.3.
3.1.8.3 time censoredtime censored, n—specimens that were still surviving when the test was terminated after elapse of a set
timeareconsideredtobetimecensored.Exampleswouldincludeexperimentswhereexposuresareconductedforapredetermined
length of time. At the end of the predetermined time, all specimens are removed from the test. Those that are still surviving are
saidtobecensored.ThisisalsoreferredtoasrightcensoredortypeIcensoring.Graphicalsolutionscanstillbeusedforparameter
estimation.Aminimum of ten observed failures should be used for estimating parameters (that is, slope and intercept, shape and
scale, etc.).
3.1.9 material propertymaterial property, n—customarily, service life is considered to be the period of time during which a
systemmeetscriticalspecifications.Correctmeasurementsareessentialtoproducemeaningfulandaccurateservicelifeestimates.
3.1.9.1 Discussion—There exists manyASTM recognized and standardized measurement procedures for determining material
properties.These practices have been developed within committees having appropriate expertise, therefore, no further elaboration
will be provided.
3.1.10 R(t)R(t), n—the probability that a random unit drawn from the population will survive at least until time (t).Also R (t)
= the fraction of units in the population that will survive at least until time (t); R (t)=1− F (t).
3.1.11 usage stressusage stress, n—the level of the experimental variable that is considered to represent the stress occurring in
normal use. This value must be determined quantitatively for accurate estimates to be made. In actual practice, usage stress may
be highly variable, such as those encountered in outdoor environments.
3.1.12 Weibull distributionWeibull distribution, n—for the purposes of this guide, theWeibull distribution is represented by the
equation:
t b
S D
F t! 51 2e c (1)
~
where:
F(t) = probability of failure by time (t) as defined in 3.1.7,
t = units of time used for service life,
c = scale parameter, and
b = shape parameter.
3.1.12.1 Discussion—The shape parameter (b), 3.1.12, is so called because this parameter determines the overall shape of the
curve. Examples of the effect of this parameter on the distribution curve are shown in Fig. 1.
3.1.12.2 Discussion—Thescaleparameter(c),3.1.12,issocalledbecauseitpositionsthedistributionalongthescaleofthetime
axis. It is equal to the time for 63.2% failure.
-1
NOTE 1—This is arrived at by allowing t to equal c in Eq 1. This then reduces to Failure Probability=1− e . which further reduces to equal 1 −
0.368 or 0.632.
4. Significance and Use
4.1 Thenatureofacceleratedservicelifeestimationnormallyrequiresthatstresseshigherthanthoseexperiencedduringservice
conditions are applied to the material being evaluated. For non-constant use stress, such as experienced by time varying weather
outdoors, it may in fact be useful to choose an accelerated stress fixed at a level slightly lower than (say 90% of) the maximum
experienced outdoors. By controlling all variables other than the one used for accelerating degradation, one may model the
expected effect of that variable at normal, or usage conditions. If laboratory accelerated test devices are used, it is essential to
provide precise control of the variables used in order to obtain useful information for service life prediction. It is assumed that the
same failure mechanism operating at the higher stress is also the life determining mechanism at the usage stress. It must be noted
that the validity of this assumption is crucial to the validity of the final estimate.
4.2 Accelerated service life test data often show different distribution shapes than many other types of data. This is due to the
effects of measurement error (typically normally distributed), combined with those unique effects which skew service life data
G172 – 03 (2010)
FIG. 1 Effect of the Shape Parameter (b) on the Weibull Probability Density
towardsearlyfailuretime(infantmortalityfailures)orlatefailuretimes(agingorwear-outfailures).Applicationsoftheprinciples
in this guide can be helpful in allowing investigators to interpret such data.
4.3 The choice and use of a particular acceleration model and life distribution model should be based primarily on how well
it fits the data and whether it leads to reasonable projections when extrapolating beyond the range of data. Further justification for
selecting models should be based on theoretical considerations.
NOTE 2—Accelerated service life or reliability data analysis packages are becoming more readily available in common computer software packages.
This makes data reduction and analyses more directly accessible to a growing number of investigators.This is not necessarily a good thing as the ability
to perform the mathematical calculation, without the fundamental understanding of the mechanics may produce some serious errors. See Ref (1).
5. Data Analysis
5.1 Overview—It is critical to the accuracy of Service Life Prediction estimates based on accelerated tests that the failure
mechanismoperatingattheacceleratedstressbethesameasthatactingatusagestress.Increasingstress(es),suchastemperature,
to high levels may introduce errors due to several factors. These include, but are not limited to, a change of failure mechanism,
changes in physical state, such as change from the solid to glassy state, separation of homogenous materials into two or more
components, migration of stabilizers or plasticisers within the material, thermal decomposition of unstable components and
formation of new materials which may react differently from the original material.
5.2 A variety of factors act to produce deviations from the expected values. These factors may be of purely a random nature
and act to either increase or decrease service life depending on the magnitude and nature of the effect of the factor. The purity of
a lubricant is an example of one such factor. An oil clean and free of abrasives and corrosive materials would be expected to
prolongtheservicelifeofamovingpartsubjecttowear.Acontaminatedoilmightprovetobeharmfulandtherebyshortenservice
life. Purely random variation in an aging factor that can either help or harm a service life might lead to a normal, or gaussian,
distribution. Such distributions are symmetrical about a central tendency, usually the mean.
5.2.1 Some non-random factors act to skew service life distributions. Defects are generally thought of as factors that can only
decrease service life (that is, monotonically decreasing performance). Thin spots in protective coatings, nicks in extruded wires,
chemical contamination in thin metallic films are examples of such defects that can cause an overall failure even though the bulk
of the material is far from failure. These factors skew the service life distribution towards early failure times.
5.2.2 Factorsthatskewservicelifetowardsgreatertimesalsoexist.Preventivemaintenanceonatestmaterial,highqualityraw
materials,reducedimpurities,andinhibitorsorotheradditivesaresuchfactors.Thesefactorsproducelifetimedistributionsshifted
The boldface numbers in parentheses refer to the list of references at the end of this standard.
G172 – 03 (2010)
towards increased longevity and are those typically found in products having a relatively long production history.
5.3 Failure Distribution—There are two main elements to the data analysis forAccelerated Service Life Predictions. The first
element is determining a mathematical description of the life time distribution as a function of time. The Weibull distribution has
been found to be the most generally useful.As Weibull parameter estimations are treated in some detail in Guide G166, they will
not be covered in depth here. It is the intention of this guide that it be used in conjunction with Guide G166. The methodology
presented herein demonstrates how to integrate the information from Guide G166 with accelerated test data. This integration
permits estimates of service life to be made with greater precision and accuracy as well as in less time than would
...









Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.