ASTM C1548-02(2007)
(Test Method)Standard Test Method for Dynamic Young's Modulus, Shear Modulus, and Poisson's Ratio of Refractory Materials by Impulse Excitation of Vibration
Standard Test Method for Dynamic Young's Modulus, Shear Modulus, and Poisson's Ratio of Refractory Materials by Impulse Excitation of Vibration
SIGNIFICANCE AND USE
This test method is non-destructive and is commonly used for material characterization and development, design data generation, and quality control purposes. The test assumes that the properties of the specimen are perfectly isotropic, which may not be true for some refractory materials. The test also assumes that the specimen is homogeneous and elastic. Specimens that are micro-cracked are difficult to test since they do not yield consistent results. Specimens with low densities have a damping effect and are easily damaged locally at the impact point. Insulating bricks can generally be tested with this technique, but fibrous insulating materials are generally too weak and soft to test.
For quality control use, the test method may be used for measuring only resonant frequencies of any standard size specimen. An elastic modulus calculation may not be needed or even feasible if the shape is non-standard, such as a slide gate plate containing a hole. Since specimens will vary in both size and mass, acceptable frequencies for each shape and material must be established from statistical data.
Dimensional variations can have a significant effect on modulus values calculated from the frequency measurements. Surface grinding may be required to bring some materials into the specified tolerance range.
Since cylindrical shapes are not commonly made from refractory materials they are not covered by this test method, but are covered in Test Method C 215.
SCOPE
1.1 This test method covers the measurement of the fundamental resonant frequencies for the purpose of calculating the dynamic Young's modulus, the dynamic shear modulus (also known as the modulus of rigidity), and the dynamic Poisson's ratio of refractory materials at ambient temperatures. Specimens of these materials possess specific mechanical resonant frequencies, which are determined by the elastic modulus, mass, and geometry of the test specimen. Therefore, the dynamic elastic properties can be computed if the geometry, mass, and mechanical resonant frequencies of a suitable specimen can be measured. The dynamic Young's modulus is determined using the resonant frequency in the flexural mode of vibration and the dynamic shear modulus is determined using the resonant frequency in the torsional mode of vibration. Poisson's ratio is computed from the dynamic Young's modulus and the dynamic shear modulus.
1.2 Although not specifically described herein, this method can also be performed at high temperatures with suitable equipment modifications and appropriate modifications to the calculations to compensate for thermal expansion.
1.3 The values are stated in SI units and are to be regarded as the standard.
1.4 This standard may involve hazardous materials, operations, and equipment. This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation:C1548–02 (Reapproved 2007)
Standard Test Method for
Dynamic Young’s Modulus, Shear Modulus, and Poisson’s
Ratio of Refractory Materials by Impulse Excitation of
Vibration
This standard is issued under the fixed designation C1548; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope C215 Test Method for Fundamental Transverse, Longitudi-
nal, and Torsional Resonant Frequencies of Concrete
1.1 This test method covers the measurement of the funda-
Specimens
mental resonant frequencies for the purpose of calculating the
C885 Test Method for Young’s Modulus of Refractory
dynamic Young’s modulus, the dynamic shear modulus (also
Shapes by Sonic Resonance
known as the modulus of rigidity), and the dynamic Poisson’s
C1259 Test Method for Dynamic Young’s Modulus, Shear
ratio of refractory materials at ambient temperatures. Speci-
Modulus, and Poisson’s Ratio for Advanced Ceramics by
mens of these materials possess specific mechanical resonant
Impulse Excitation of Vibration
frequencies, which are determined by the elastic modulus,
mass, and geometry of the test specimen. Therefore, the
3. Summary of Test Method
dynamic elastic properties can be computed if the geometry,
3.1 The fundamental resonant frequencies are determined
mass, and mechanical resonant frequencies of a suitable
by measuring the resonant frequency of specimens struck once
specimen can be measured. The dynamic Young’s modulus is
mechanically with an impacting tool. Frequencies are mea-
determined using the resonant frequency in the flexural mode
sured with a transducer held lightly against the specimen using
of vibration and the dynamic shear modulus is determined
a signal analyzer circuit. Impulse and transducer locations are
usingtheresonantfrequencyinthetorsionalmodeofvibration.
selected to induce and measure one of two different modes of
Poisson’s ratio is computed from the dynamic Young’s modu-
vibration. The appropriate resonant frequencies, dimensions,
lus and the dynamic shear modulus.
and mass of each specimen may be used to calculate dynamic
1.2 Although not specifically described herein, this method
Young’s modulus, dynamic shear modulus, and dynamic Pois-
can also be performed at high temperatures with suitable
son’s ratio.
equipment modifications and appropriate modifications to the
calculations to compensate for thermal expansion.
4. Significance and Use
1.3 The values are stated in SI units and are to be regarded
4.1 This test method is non-destructive and is commonly
as the standard.
used for material characterization and development, design
1.4 This standard may involve hazardous materials, opera-
data generation, and quality control purposes.The test assumes
tions, and equipment. This standard does not purport to
that the properties of the specimen are perfectly isotropic,
address all of the safety concerns, if any, associated with its
which may not be true for some refractory materials. The test
use. It is the responsibility of the user of this standard to
also assumes that the specimen is homogeneous and elastic.
establish appropriate safety and health practices and deter-
Specimensthataremicro-crackedaredifficulttotestsincethey
mine the applicability of regulatory limitations prior to use.
do not yield consistent results. Specimens with low densities
2. Referenced Documents have a damping effect and are easily damaged locally at the
2 impactpoint.Insulatingbrickscangenerallybetestedwiththis
2.1 ASTM Standards:
technique, but fibrous insulating materials are generally too
C71 Terminology Relating to Refractories
weak and soft to test.
4.2 For quality control use, the test method may be used for
This test method is under the jurisdiction of ASTM Committee C08 on
measuring only resonant frequencies of any standard size
Refractories and is the direct responsibility of Subcommittee C08.01 on Strength.
specimen.Anelasticmoduluscalculationmaynotbeneededor
Current edition approved March 1, 2007. Published April 2007. Originally
even feasible if the shape is non-standard, such as a slide gate
approved in 2002. Last previous edition approved in 2002 as C1548 – 02. DOI:
10.1520/C1548-02R07.
plate containing a hole. Since specimens will vary in both size
For referenced ASTM standards, visit the ASTM website, www.astm.org, or
and mass, acceptable frequencies for each shape and material
contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
must be established from statistical data.
Standards volume information, refer to the standard’s Document Summary page on
the ASTM website.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
C1548–02 (2007)
4.3 Dimensional variations can have a significant effect on 5.3 Specimen Support—The support shall permit the speci-
modulus values calculated from the frequency measurements. men to vibrate freely without restricting the desired mode of
Surface grinding may be required to bring some materials into vibration. For room temperature measurements, soft rubber or
the specified tolerance range. plastic strips located at the nodal points are typically used.
4.4 Since cylindrical shapes are not commonly made from Alternately, the specimen can be placed on a thick soft rubber
refractory materials they are not covered by this test method, pad. For elevated temperature measurements, the specimen
but are covered in Test Method C215. may be suspended from support wires wrapped around the
specimen at nodal points and passing vertically out of the test
5. Apparatus
chamber.
5.1 Electronic System—The electronic system in Fig. 1
6. Test Specimen
consists of a signal conditioner/amplifier, a signal analyzer, a
6.1 Preparation—Test specimens shall be prepared to yield
frequency readout device, and a signal transducer for sensing
uniform rectangular shapes. Normally, brick sized specimens
the vibrations. The system should have sufficient precision to
are used. Although smaller bars cut from bricks are easily
measure frequencies to an accuracy of 0.1 %. Commercial
tested for flexural resonant frequencies, it is more difficult to
instrumentation is available which meets this requirement.
obtain torsional resonance in specimens of square cross-
5.1.1 Frequency Analyzer—This consists of a signal
section. Some pressed brick shapes are dimensionally uniform
conditioner/amplifier to power the transducer and a digital
enough to test without surface grinding, but specimens cut
waveform analyzer or frequency counter with storage capabil-
from larger shapes or prepared by casting or other means often
ity to analyze the signal from the transducer. The waveform
require surface grinding of one or more surfaces to meet the
analyzer shall have a sampling rate of at least 20 000 Hz. The
dimensional criteria noted below.
frequency counter should have an accuracy of 0.1 %.
6.2 Heat Treatment—All specimens shall be prefired to the
5.1.2 Sensor—Apiezeoelectric accelerometer contact trans-
desired temperature and oven dried before testing.
ducer is most commonly used, although non-contact transduc-
6.3 Dimensional Ratios—Specimens having either very
ers based on acoustic, magnetic, or capacitance measurements
small or very large ratios of length to maximum transverse
may also be used. The transducer shall have a frequency
dimensions are frequently difficult to excite in the fundamental
response in the range of 50 Hz to 10 000 Hz, and have a
modes of vibration. Best results are obtained when this ratio is
resonant frequency above 20 000 Hz. The sensor shall have a
between 3 and 5. For use of the equations in this method, the
mark identifying the maximum sensitivity direction so that it
ratio must be at least 2.
can be properly oriented for each vibration mode.
6.4 Dimensional Uniformity—Rectangular specimens shall
5.2 Impactor—Because refractory materials are tested with
have surfaces that are flat and parallel to within 6 0.5 % of the
specimens of various sizes, it is not feasible to specify an
nominal measured value.
impactor with a specific size, weight, or construction method.
6.5 Weight (or Mass) and Dimensions—Determine the
However, hammer style impactors which have light weight
weight (or mass) to the nearest 6 0.5 %. Measure each
handles with the impacting mass concentrated near the end are
dimension to within 6 0.5 %.
preferred to dropping vertical impactors. Steel hammer style
impactors, with head weights between 0.3 and 3 % of the
7. Measurement of Impulse Resonant Frequencies
specimen weight, are recommended. To avoid damaging the
7.1 Transverse Frequency:
surface of insulating bricks or other weak materials, plastic or
7.1.1 Support the specimen so that it may vibrate freely in
rubber shapes should be substituted for the steel impactors.
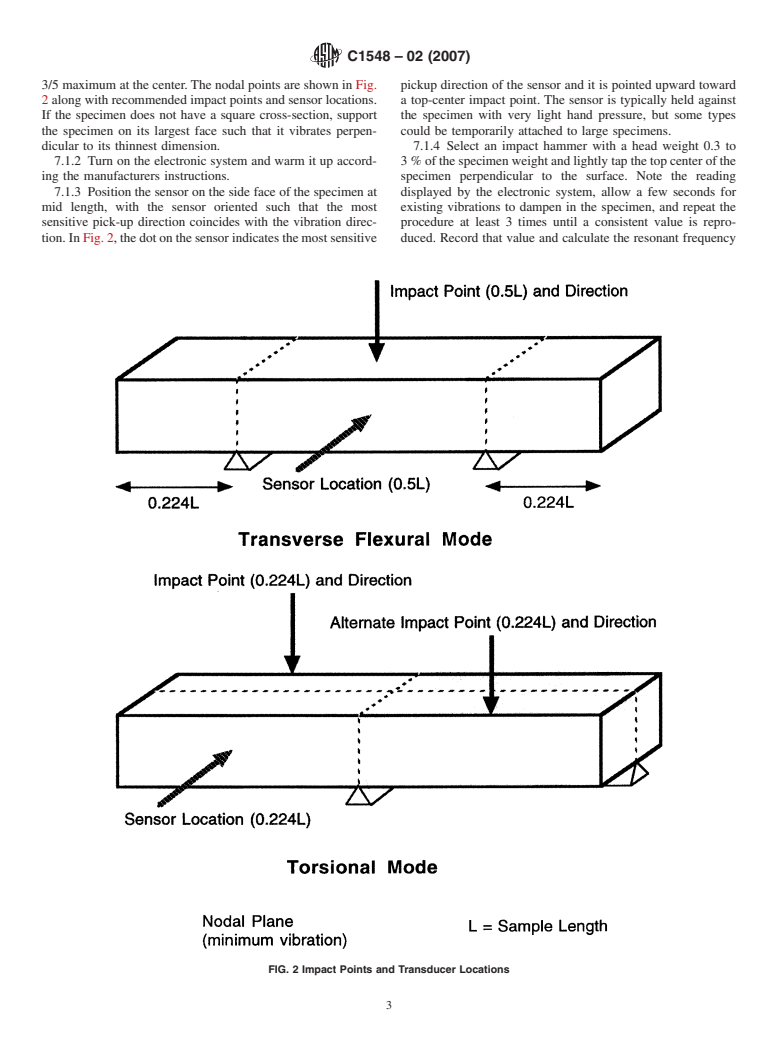
thefundamentaltransversemode.Inthismodethenodalpoints
(where the displacement is zero) are located at 0.224L from
each end, where Lis the specimen length.Vibrationaldisplace-
Equipment found suitable is available from J. W. Lemmons, Inc., 3466
ments are a maximum at the ends of the specimen and about
Bridgeland Drive, Suite 230, St. Louis, MO 63044-260.
FIG. 1 Diagram of Test Apparatus
C1548–02 (2007)
3/5 maximum at the center. The nodal points are shown in Fig. pickup direction of the sensor and it is pointed upward toward
2 along with recommended impact points and sensor locations. a top-center impact point. The sensor is typically held against
If the specimen does not have a square cross-section, support the specimen with very light hand pressure, but some types
the specimen on its largest face such that it vibrates perpen- could be temporarily attached to large specimens.
dicular to its thinnest dimension. 7.1.4 Select an impact hammer with a head weight 0.3 to
7.1.2 Turn on the electronic system and warm it up accord- 3 %ofthespecimenweightandlightlytapthetopcenterofthe
ing the manufacturers instructions. specimen perpendicular to the surface. Note the reading
7.1.3 Position the sensor on the side face of the specimen at displayed by the electronic system, allow a few seconds for
mid length, with the sensor oriented such that the most existing vibrations to dampen in the specimen, and repeat the
sensitive pick-up direction coincides with the vibration direc- procedure at least 3 times until a consistent value is repro-
tion.InFig.2,thedotonthesensorindicatesthemostsensitive duced. Record that value and calculate the resonant frequency
FIG. 2 Impact Points and Transducer Locations
C1548–02 (2007)
t
from it per the manufacturer’s instructions if frequency is not
8.340 ~1 1 0.2023µ 1 2.173µ !
HS S D DJ
L
displayed directly. If a consistent value cannot be obtained,
t
either the specimen is damaged or other modes of vibration are 2
1.000 1 6.338 1 1 0.1408µ 1 1.536µ !
~
HS S D DJ
L
interfering with the measurement.
7.2 Torsional Frequency
µ = Poisson’s ratio.
7.2.1 Support the specimen so that it may vibrate freely in
8.1.1.1 If L / t$ 20, T can be simplified to:
torsion. In this mode there is a single nodal point at the center
and vibrations are a maximum at the ends. The impact and 2
t
T 5 1.000 1 6.585
S S D D
sensor pickup points are located at 0.224L from the ends. This L
location is a nodal point for flexural vibration and minimizes
and E can be calculated directly.
interference from flexural vibrations.
8.1.1.2 If L / t < 20, then an initial Poisson’s ratio must be
7.2.2 Turn on the electronic system and warm it up accord-
assumed to start the computations.An iterative process is then
ing to the manufacturers instructions.
used to determine a value of Poisson’s ratio, based on
experimental Young’s modulus and shear modulus. This itera-
7.2.3 Position the sensor on the side face of the specimen at
0.224L,withthesensororientedsuchthatthesensitivepick-up tive process is shown in Fig. 3 and described below.
(1) Determine the fundamental flexural and torsional reso-
direction coincides with the vibration direction. In Fig. 2, the
dot on the sensor indicates the most sensitive pickup direction nant frequencies of the rectangular test specimen. Using Eq 2,
the dynamic shear modulus of the test specimen is calculated
of the sensor and it is pointed upward toward a top impact
point. from the fundamental torsional resonant frequency and the
dimension and mass of the specimen.
7.2.4 Select an impact hammer with a head weight 0.3 to
(2) Using Eq 1, the dynamic Young’s modulus of the
3 % of the specimen weight and lightly tap the top of the
rectangular test specimen is calculated from the fundamental
specimen at a 0.224L location perpendicular to the surface.
flexural resonant frequency, the dimensions and mass of the
Note the reading displayed by the electronic system, allow a
specimen, and the initial/iterative Poisson’s ratio.
few seconds for existing vibrations to dissipate, and repeat the
(3) The dynamic shear modulus and Young’s values
process at least 3 times until a consistent value is reproduced.
modulus.calculated in steps (1) and (2) are substituted into Eq
Record that value and calculate the resonant frequency from it
3, for Poisson’s ratio. A new value for Poisson’s ratio is then
if frequency is not displayed directly.
calculated for another iteration starting at step (2).
(4) Steps (2) and (3) are repeated until no significant
8. Calculations
difference (2 % or less) is observed between the last iterative
4,5
8.1 Dynamic Young’s Modulus :
value and the final computed value of the Poisson’s ratio.
8.1.1 From the fundamental flexural vibration of a rectan- Self-consistent values for the moduli are thus obtained.
6,7
gular bar: 8.2 Dynamic Shear Modulus :
8.2.1 From the fundamental torsional vibration of a rectan-
2 3
mf L
f
E 5 0.9465 T (1) gular bar:
S DS D 1
b
t
4Lmf B
~ !
t
G 5 (2)
H JH J
where:
~bt! ~1 1A!
E = Young’s modulus, Pa,
m = mass of the bar, g, where:
G = shear modulus, Pa, and
b = width of the bar, mm,
L = length of the bar, mm, f = fundamental resonant frequency of the bar in torsion,
t
t = thickness of the bar, mm,
Hz.
f = fundamental resonant frequency of the bar in flexure,
f
b t
Hz, and 1
HS D S DJ
t b
T = correction factor for fundamental flexural made to B 5
1 2 6
t t t
4 2 2.52 1 0.21
accountforfinitethicknessofbar,Poisson’sratio,etc.
H S D S D S D J
b b b
2 3
b b b
0.5062 2 0.8776 1 0.3504 2 0.0078
2 H S D S D S D J
t t
t t t
T 5 1 1 6.585 ~1 1 0.0752µ 1 0.8109µ ! 2 0.868 2
S D S D
1 A 5
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.