ASTM F1811-97

Standard Practice for Estimating the Power Spectral Density Function and Related Finish Parameters from Surface Profile Data

SCOPE
1.1 This practice defines the methodology for calculating a set of commonly used statistical parameters and functions of surface roughness from a set of measured surface profile data. Its purposes are to provide fundamental procedures and notation for processing and presenting data, to alert the reader to related issues that may arise in user-specific applications, and to provide literature references where further details can be found.

General Information

• Status: Historical
• Publication Date: 09-Jun-1997
• Technical Committee: F01 - Electronics

Relations

• Replaced By: ASTM F1811-97(2002) - Standard Practice for Estimating the Power Spectral Density Function and Related Finish Parameters from Surface Profile Data (Withdrawn 2003)
• Effective Date: 10-Jun-1997

Standards Content (Sample)

NOTICE: This standard has either been superceded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
Designation: F 1811 – 97
Standard Practice for
Estimating the Power Spectral Density Function and Related
Finish Parameters from Surface Profile Data
This standard is issued under the fixed designation F 1811; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
1. Scope profile across the surface, or the “ensemble” average of an
infinite number of finite-length profiles. In contrast, real profile
1.1 This practice defines the methodology for calculating a
data are available in the form of one or more sets of digitized
set of commonly used statistical parameters and functions of
height data measured at a finite number of discrete positions on
surface roughness from a set of measured surface profile data.
the surface under test. This practice gives both the abstract
Its purposes are to provide fundamental procedures and nota-
definitions of the statistical quantities of interest, and numerical
tion for processing and presenting data, to alert the reader to
procedures for determining values of these abstract quantities
related issues that may arise in user-specific applications, and
from sets of measured data. In the notation of this practice
to provide literature references where further details can be
these numerical procedures are called “estimators” and the
found.
results that they produce are called “estimates”.
1.2 The present practice is limited to the analysis of one-
1.6 This practice gives “periodogram” estimators for deter-
dimensional or profile data taken at uniform intervals along
mining the root-mean-square (rms) roughness, rms slope, and
straight lines across the surface under test, although reference
power spectral density (PSD) of the surface directly from
is made to the more general case of two-dimensional measure-
profile height or slope measurements. The statistical literature
ments made over a rectangular array of data points.
uses a circumflex to distinguish an estimator or estimate from
1.3 The data analysis procedures described in this practice
its abstract or ensemble-average value. For example, Â denotes
are generic and are not limited to specific surfaces, surface-
an estimate of the quality A. However, some word-processors
generation techniques, degrees of roughness, or measuring
cannot place a circumflex over consonants in text. Any
techniques. Examples of measuring techniques that can be used
symbolic or verbal device may be used instead.
to generate profile data for analysis are mechanical profiling
1.7 The quality of estimators of surface statistics are, in
instruments using a rigid contacting probe, optical profiling
turn, characterized by higher-order statistical properties that
instruments that sample over a line or an array over an area of
describe their “bias” and “fluctuation” properties with respect
the surface, optical interferometry, and scanning-microscopy
to their abstract or ensemble-average versions. This practice
techniques such as atomic-force microscopy. The distinctions
does not discuss the higher-order statistical properties of the
between different measuring techniques enter the present
estimators given here since their practical significance and use
practice through various parameters and functions that are
are application-specific and beyond the scope of this document.
defined in Sections 3 and 5, such as their sampling intervals,
Details of these and related subjects can be found in References
bandwidths, and measurement transfer functions.
(1–10) at the end of this practice.
1.4 The primary interest here is the characterization of
1.8 Raw measured profile data generally contain trending
random or periodic aspects of surface finish rather than isolated
components that are independent of the microtopography of the
surface defects such as pits, protrusions, scratches or ridges.
surface being measured. These components must be subtracted
Although the methods of data analysis described here can be
before the difference or residual errors are subjected to the
equally well applied to profile data of isolated surface features,
statistical-estimation routines given here. These trending com-
the parameters and functions that are derived using the
ponents originate from both extrinsic and intrinsic sources.
procedures described in this practice may have a different
Extrinsic trends arise from the rigid-body positioning of the
physical significance than those derived from random or
part under test in the measuring apparatus. In optics these
periodic surfaces.
displacement and rotation contributions are called “piston” and
1.5 The statistical parameters and functions that are dis-
“tilt” errors. In contrast, intrinsic trends arise from deliberate or
cussed in this practice are, in fact, mathematical abstractions
accidental shape errors inherent in the surface under test, such
that are generally defined in terms of an infinitely-long linear
as a circular or parabolic curvature. In the absence of a-priori
information about the true surface shape, the intrinsic shape
This practice is under the jurisdiction of ASTM Committee F-1 on Electron-
icsand is the direct responsibility of Subcommittee F01.06 on Silicon Materials and
Process Control. The boldface numbers in parentheses refer to the list of references at the end of
Current edition approved June 10, 1997. Published August 1997. this practice.
Copyright © ASTM, 100 Barr Harbor Drive, West Conshohocken, PA 19428-2959, United States.
NOTICE: This standard has either been superceded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
F 1811
error is frequently limited to a quadratic (parabolic) curvature parameters or functions generated by the procedures described
of the surface. Detrending of intrinsic and extrinsic trends is
herein be accompanied by an identifying description of mea-
generally accomplished simultaneously by subtracting a de- suring instrument used, estimates of its low- and high-
trending polynomial from the raw measured data, where the
frequency limits, LFL and HFL, and a statement of whether or
polynomial coefficients are determined by least-squares fitting not restoration techniques were used.
to the measured data.
1.13 In order to make a quantitative comparison between
1.9 Although surfaces and surface measuring instruments
profile data obtained from different measurement techniques,
exist in real or configuration space, they are most easily
the statistical parameters and functions of interest must be
understood in frequency space, also known as Fourier trans-
compared over the same or comparable spatial-frequency
form, reciprocal or spatial-frequency space. This is because
regions. The most common quantities used to compare surfaces
any practical measurement process can be considered to be a
are their root-mean-square (rms) roughness values, which are
“linear system”, meaning that the measured profile is the
the square roots of the areas under the PSD between specified
convolution of the true surface profile and the impulse response
surface-frequency limits. Surface statistics derived from mea-
of the measuring system; and equivalently, the Fourier-
surements involving different spatial-frequency ranges cannot
amplitude spectrum of the measured profile is the product of
be compared quantitatively except in an approximate way. In
that of the true profile and the frequency-dependent “transfer
some cases measurements with partially or even nonoverlap-
function” of the measurement system. This is expressed
ping bandwidths can be compared by using analytic models of
symbolically by the following equation:
the PSDs to extrapolate the PSDs outside their measurement
A ~ f ! 5 A ~ f ! · T ~f ! bandwidth.
meas x true x x
1.14 Examples of specific band-width limits can be drawn
where:
from the optical and semiconductor industries. In optics the
A = the Fourier amplitudes,
so-called total integrated scatter or TIS measurement technique
T( f ) = instrument response function or the measurement
x
leads to rms roughness values involving an annulus in two-
transfer function, and
–1
dimensional spatial frequencies space from 0.069 to 1.48 μm ;
f = surface spatial frequency.
x
that is, a dynamic range of 1.48/0.069 = 21/1. In contrast, the
This factorization permits the surface and the measuring
range of spatial frequencies involved in optical and mechanical
system to be discussed independently of each other in fre-
scanning techniques are generally much larger than this,
quency space, and is an essential feature of any discussion of
frequently having a dynamic ranges of 512/1 or more. In the
measurement systems.
–1
latter case the subrange of 0.0125 to 1 μm has been used to
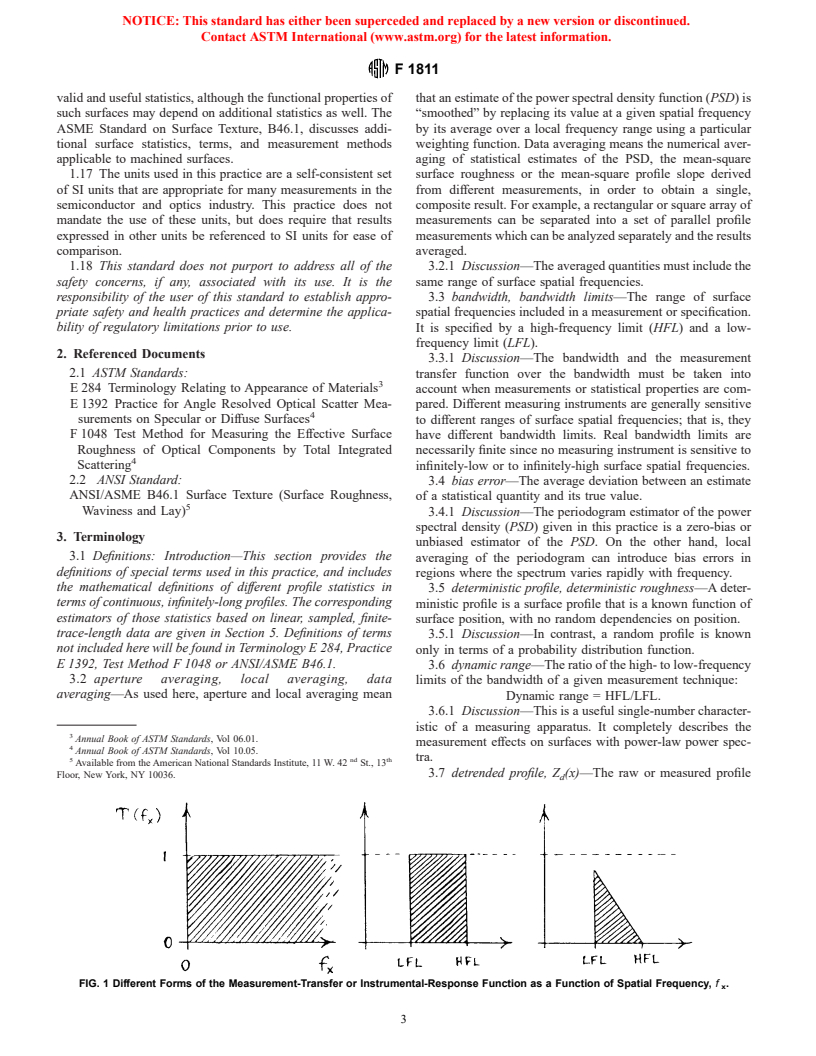
1.10 Figure 1 sketches different forms of the measurement
discuss the rms surface roughness in the semiconductor indus-
transfer function, T( f ):
x
try. These numbers are provided to illustrate the magnitudes
1.10.1 Case (a) is a perfect measuring system, which has
and ranges of HFL and LFL encountered in practice but do not
T ( f ) = 1 for all spatial frequencies, 0 # f # ‘ . This is
x x
constitute a recommendation of particular limits for the speci-
unrealistic since no real measuring instrument is equally
fication of surface finish parameters. Such selections are
sensitive to all spatial frequencies. Case (b) is an ideal mea-
application dependent, and are to be made at the users’
suring system, which has T (f )=1for LFL # f # HFL and
x x
discretion.
T (f ) = 0 otherwise, where LFL and HFL denote the
x
1.15 The limits of integration involved in the determination
low-frequency and high-frequency limits of the measurement.
of rms roughness and slope values from measured profile data
The range LFL # f # HFL is called the bandpass or
x
are introduced by multiplying the measured PSD by a factor
bandwidth of the measurement, and ratio HFL/LFL is called
equal to zero for spatial frequencies outside the desired
the dynamic range of the measurement. Case (c) represents a
bandpass and unity within the desired bandpass, as shown in
realistic measuring system, since it includes the fact that T (f )
x
Case (b) in Fig. 1. This is called a top-hat or binary filter
need not be unity within the measurement bandpass or strictly
function. Before the ready availability of digital frequency-
zero outside the bandpass.
domain processing as employed in this practice, bandwidth
1.11 If the measurement transfer function is known to
limits were imposed by passing the profile data through analog
deviate significantly from unity within the measurement band-
or digital filters without explicitly transforming them into the
pass, the measured power spectral density (PSD) can be
frequency domain and multiplying by a top-hat function. The
transformed into the form that would have been measured by
two processes are mathematically equivalent, providing the
an instrument with the ideal rectangular form through the
data filter has the desired frequency response. Real data filters,
process of digital “restoration.” In its simplest form restoration
however, frequently have Gaussian or RC forms that only
involves dividing the measured PSD by the known form of
approximate the desired top-hat form that introduces some
?T ~ f ! ? over the measurement bandpass. Restoration is par-
x
ambiguity in their interpretation. This practice recommends the
ticularly relevant to measuring instruments that involve optical
determination of rms roughness and slope values using top-hat
microscopes since the transfer functions of microscope systems
windowing of the measured PSD in the frequency domain.
are not unity over their bandpass but tend to fall linearly
between unity at T (0) = 1 and T(HFL) = 0. The need for, and 1.16 The PSD and rms roughness are surface statistics of
methodology of digital restoration is instrument specific and particular interest to the optics and semiconductor industries
this practice places no requirements on its use. because of their direct relationship to the functional properties
1.12 This practice requires that any data on surface finish of such surfaces. In the case of rougher surfaces these are still
NOTICE: This standard has either been superceded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
F 1811
valid and useful statistics, although the functional properties of that an estimate of the power spectral density function (PSD)is
such surfaces may depend on additional statistics as well. The “smoothed” by replacing its value at a given spatial frequency
ASME Standard on Surface Texture, B46.1, discusses addi- by its average over a local frequency range using a particular
tional surface statistics, terms, and measurement methods weighting function. Data averaging means the numerical aver-
applicable to machined surfaces. aging of statistical estimates of the PSD, the mean-square
1.17 The units used in this practice are a self-consistent set surface roughness or the mean-square profile slope derived
of SI units that are appropriate for many measurements in the from different measurements, in order to obtain a single,
semiconductor and optics industry. This practice does not composite result. For example, a rectangular or square array of
mandate the use of these units, but does require that results measurements can be separated into a set of parallel profile
expressed in other units be referenced to SI units for ease of measurements which can be analyzed separately and the results
comparison. averaged.
1.18 This standard does not purport to address all of the 3.2.1 Discussion—The averaged quantities must include the
safety concerns, if any, associated with its use. It is the same range of surface spatial frequencies.
responsibility of the user of this standard to establish appro- 3.3 bandwidth, bandwidth limits—The range of surface
priate safety and health practices and determine the applica- spatial frequencies included in a measurement or specification.
bility of regulatory limitations prior to use. It is specified by a high-frequency limit (HFL) and a low-
frequency limit (LFL).
2. Referenced Documents
3.3.1 Discussion—The bandwidth and the measurement
2.1 ASTM Standards:
transfer function over the bandwidth must be taken into
E 284 Terminology Relating to Appearance of Materials account when measurements or statistical properties are com-
E 1392 Practice for Angle Resolved Optical Scatter Mea-
pared. Different measuring instruments are general
...