ASTM E1325-16
(Terminology)Standard Terminology Relating to Design of Experiments
Standard Terminology Relating to Design of Experiments
ABSTRACT
This standard includes those statistical items related to the area of design of experiments for which standard definitions appear desirable. It provides definitions, descriptions, discussion, and comparison of terms.
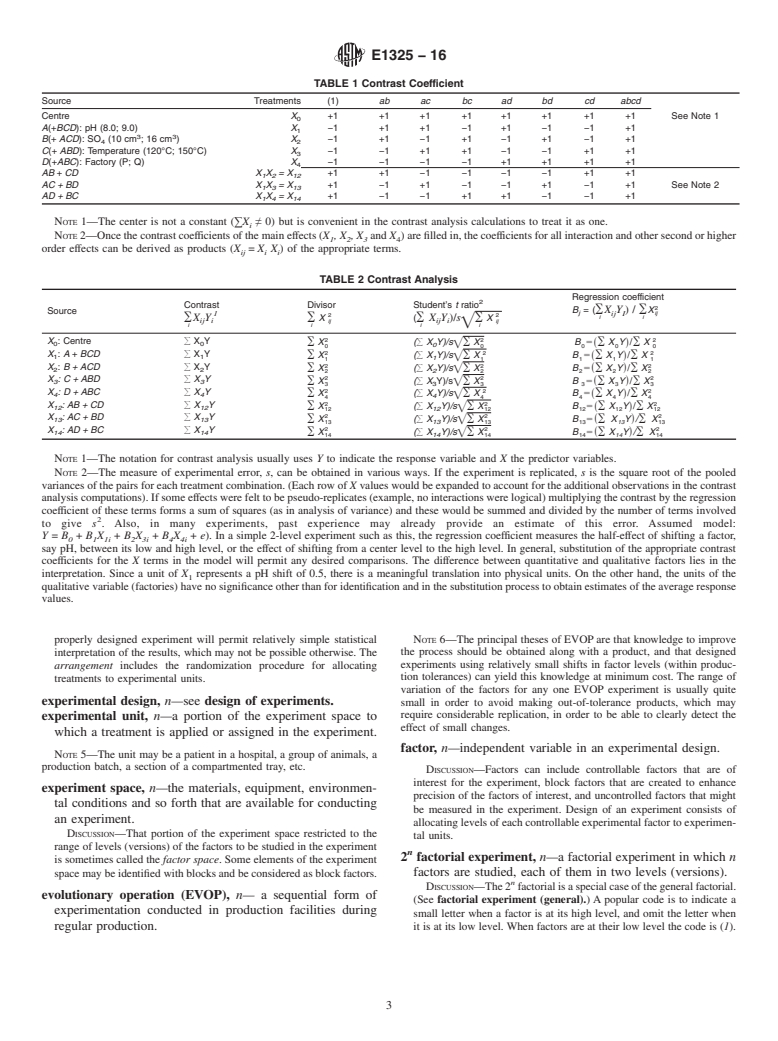
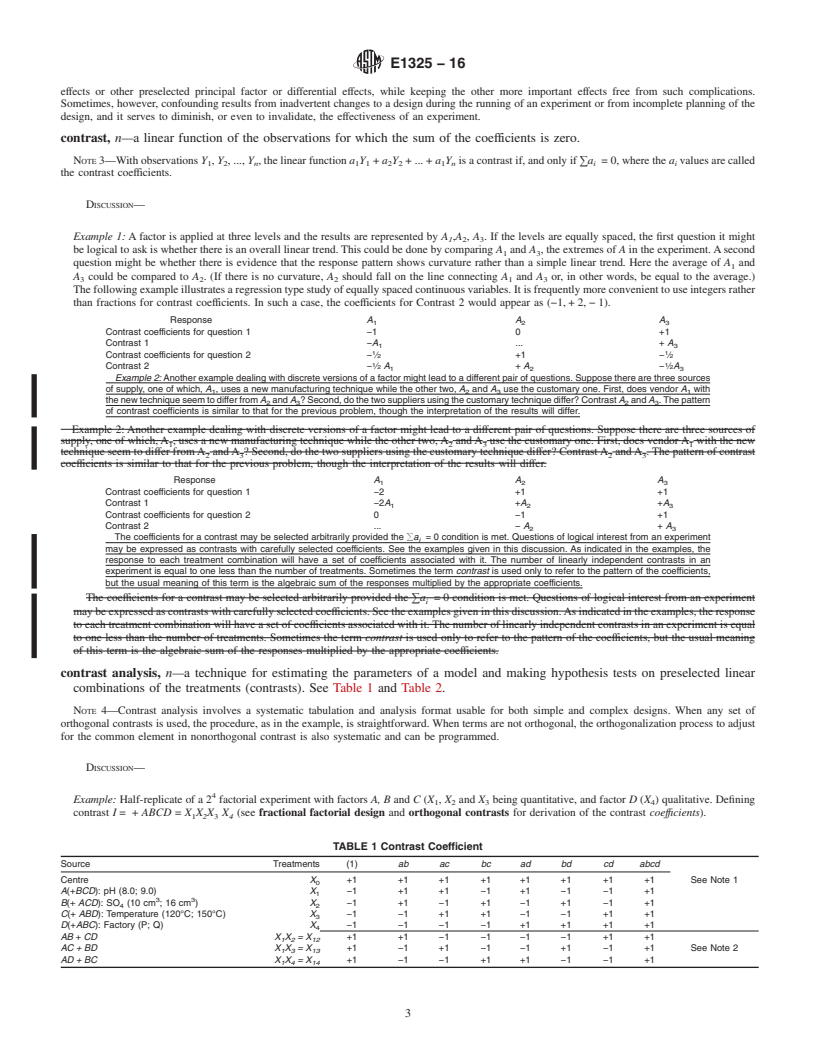
This standard also provides the table of contrast coefficient and table of contrast analysis. The table of contrast coefficient implies that once the contrast coefficients of the main effects (X1, X2, X3 and X4) are filled in, the coefficients for all interaction and other second or higher order effects can be derived as products (Xij = Xi Xi) of the appropriate terms. The table on contrast analysis indicates the measure of experimental error, s, that can be obtained in various ways. If the experiment is replicated, s is the square root of the pooled variances of the pairs for each treatment combination. If some effects were felt to be pseudo-replicates, multiplying the contrast by the regression coefficient of these terms forms a sum of squares (as in analysis of variance) and these would be summed and divided by the number of terms involved to give s².
SIGNIFICANCE AND USE
3.1 This standard is a subsidiary to Terminology E456.
3.2 It provides definitions, descriptions, discussion, and comparison of terms.
SCOPE
1.1 This standard includes those statistical items related to the area of design of experiments for which standard definitions appear desirable.
General Information
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E1325 − 16 An American National Standard
Standard Terminology Relating to
1
Design of Experiments
This standard is issued under the fixed designation E1325; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope k of different versions from the t versions of a single
principal factor arranged so that every pair of versions
1.1 This standard includes those statistical items related to
occurs together in the same number, λ, of blocks from the b
the area of design of experiments for which standard defini-
blocks.
tions appear desirable.
DISCUSSION—The design implies that every version of the principal
factor appears the same number of times r in the experiment and that
2. Referenced Documents
the following relations hold true: bk = tr and r (k−1)=λ(t − 1).
2
2.1 ASTM Standards:
For randomization, arrange the blocks and versions within each
blockindependentlyatrandom.Sinceeachletterintheaboveequations
E456Terminology Relating to Quality and Statistics
represents an integer, it is clear that only a restricted set of combina-
tions(t, k, b, r,λ)ispossibleforconstructingbalancedincompleteblock
3. Significance and Use
designs. For example, t =7, k =4, b =7, λ=2. Versions of the
3.1 This standard is a subsidiary to Terminology E456.
principal factor:
3.2 It provides definitions, descriptions, discussion, and
Block1 1236
2 2347
comparison of terms.
3 3451
4 4562
4. Terminology
5 5673
6 6714
aliases, n—in a fractional factorial design,twoormoreeffects
7 7125
which are estimated by the same contrast and which,
therefore, cannot be estimated separately.
block factor, n—a factor that indexes division of experimental
n
DISCUSSION—(1) The determination of which effects in a 2 factorial
units into disjoint subsets.
are aliasedcanbemadeoncethe defining contrast(inthecaseofahalf
1
replicate) or defining contrasts (for a fraction smaller than ⁄2) are
DISCUSSION—Blocks are sets of similar experimental units intended
stated. The defining contrast is that effect (or effects), usually thought
tomakevariabilitywithinblocksassmallaspossible,sothattreatment
tobeofnoconsequence,aboutwhichallinformationmaybesacrificed
effects will be more precisely estimated. The effect of a block factor is
fortheexperiment.Anidentity, I,isequatedtothe defining contrast(or
usually not of primary interest in the experiment. Components of
2 2 2
defining contrasts) and, using the conversion that A = B = C = I, the
varianceattributabletoblocksmaybeofinterest.Theoriginoftheterm
multiplication of the letters on both sides of the equation shows the
“block” is in agricultural experiments, where a block is a contiguous
aliases.Intheexampleunderfractionalfactorialdesign, I =ABCD.So
portion of a field divided into experimental units, “plots,” that are each
2 2 2
that: A = A BCD = BCD, and AB = A B CD=CD.
subjected to a treatment.
(2) With a large number of factors (and factorial treatment combi-
1 1
nations) the size of the experiment can be reduced to ⁄4, ⁄8,orin
completely randomized design, n—a design in which the
k n-k
1
general to ⁄2 to form a 2 fractional factorial.
treatments are assigned at random to the full set of experi-
(3) There exist generalizations of the above to factorials having
mental units.
more than 2 levels.
DISCUSSION—No block factors are involved in a completely random-
ized design.
balanced incomplete block design (BIB), n—an incomplete
block design in which each block contains the same number
completely randomized factorial design, n—a factorial ex-
periment (including all replications) run in a completely
1 randomized design.
ThisterminologyisunderthejurisdictionofASTMCommitteeE11onQuality
and Statistics and is the direct responsibility of Subcommittee E11.10 on Sampling
composite design, n—a design developed specifically for
/ Statistics.
Current edition approved April 1, 2016. Published April 2016. Originally fitting second order response surfaces to study curvature,
approved in 1990. Last previous edition approved in 2015 as E1325–15. DOI:
constructed by adding further selected treatments to those
10.1520/E1325-16.
n
obtained from a 2 factorial (or its fraction).
2
For referenced ASTM standards, visit the ASTM website, www.astm.org, or
DISCUSSION—If the coded levels of each factor are−1 and+1 in the
contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
n
2 factorial(seenotation2underdiscussionfor factorial experiment),
Standards volume information, refer to the standard’s Document Summary page on
the ASTM website. the(2n +1)additionalcombinationsfora central composite designare
Copyright © ASTM Internati
...
This document is not an ASTM standard and is intended only to provide the user of an ASTM standard an indication of what changes have been made to the previous version. Because
it may not be technically possible to adequately depict all changes accurately, ASTM recommends that users consult prior editions as appropriate. In all cases only the current version
of the standard as published by ASTM is to be considered the official document.
Designation: E1325 − 15 E1325 − 16 An American National Standard
Standard Terminology Relating to
1
Design of Experiments
This standard is issued under the fixed designation E1325; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope
1.1 This standard includes those statistical items related to the area of design of experiments for which standard definitions
appear desirable.
2. Referenced Documents
2
2.1 ASTM Standards:
E456 Terminology Relating to Quality and Statistics
3. Significance and Use
3.1 This standard is a subsidiary to Terminology E456.
3.2 It provides definitions, descriptions, discussion, and comparison of terms.
4. Terminology
aliases, n—in a fractional factorial design, two or more effects which are estimated by the same contrast and which, therefore,
cannot be estimated separately.
1
This terminology is under the jurisdiction of ASTM Committee E11 on Quality and Statistics and is the direct responsibility of Subcommittee E11.10 on Sampling /
Statistics.
Current edition approved Oct. 1, 2015April 1, 2016. Published October 2015April 2016. Originally approved in 1990. Last previous edition approved in 20082015 as
E1325 – 02 (2008).E1325 – 15. DOI: 10.1520/E1325-15.10.1520/E1325-16.
2
For referenced ASTM standards, visit the ASTM website, www.astm.org, or contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM Standards
volume information, refer to the standard’s Document Summary page on the ASTM website.
DISCUSSION—
n
(1) The determination of which effects in a 2 factorial are aliased can be made once the defining contrast (in the case of a half replicate) or defining
1
contrasts (for a fraction smaller than ⁄2) are stated. The defining contrast is that effect (or effects), usually thought to be of no consequence, about which
all information may be sacrificed for the experiment. An identity, I, is equated to the defining contrast (or defining contrasts) and, using the conversion
2 2 2
that A = B = C = I, the multiplication of the letters on both sides of the equation shows the aliases. In the example under fractional factorial design,
2 2 2
I = ABCD. So that: A = A BCD = BCD, and AB = A B CD = CD.
k
1 1 1
(2) With a large number of factors (and factorial treatment combinations) the size of the experiment can be reduced to ⁄4, ⁄8, or in general to ⁄2
n-k
to form a 2 fractional factorial.
(3) There exist generalizations of the above to factorials having more than 2 levels.
balanced incomplete block design (BIB), n—an incomplete block design in which each block contains the same number k of
different versions from the t versions of a single principal factor arranged so that every pair of versions occurs together in the
same number, λ, of blocks from the b blocks.
DISCUSSION—
The design implies that every version of the principal factor appears the same number of times r in the experiment and that the following relations
hold true: bk = tr and r (k − 1) = λ(t − 1).
For randomization, arrange the blocks and versions within each block independently at random. Since each letter in the above equations represents
an integer, it is clear that only a restricted set of combinations (t, k, b, r, λ) is possible for constructing balanced incomplete block designs. For example,
t = 7, k = 4, b = 7, λ = 2. Versions of the principal factor:
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
1
---------------------- Page: 1 ----------------------
E1325 − 16
Block 1 1 2 3 6
2 2 3 4 7
3 3 4 5 1
4 4 5 6 2
5 5 6 7 3
6 6 7 1 4
7 7 1 2 5
block factor, n—a factor that indexes division of experimental units into disjoint subsets.
DISCUSSION—
Blocks are sets of similar experimental units intended to make variability within blocks as small as possible, so that treatment effects will be more
precisely estimated. The effect of a block factor is usually not of primary interest in the experiment. Components of variance attributable to blocks
may be of interest. The origin of the term “block” is in agricultural experiments, where a block is a contiguous portion of a field divided into
experimental units, “plots,” that are each subjected to a treatment.
completely randomized design, n—a design in which the treatments are assigned at random to the full set of exper
...








Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.