ASTM E1813-96e1

Standard Practice for Measuring and Reporting Probe Tip Shape in Scanning Probe Microscopy

SCOPE
1.1 This practice covers scanning probe microscopy and describes the parameters needed for probe shape and orientation.
1.2 This practice also describes a method for measuring the shape and size of a probe tip to be used in scanning probe microscopy. The method employs special sample shapes, known as probe characterizers, which can be scanned with a probe microscope to determine the dimensions of the probe. Mathematical techniques to extract the probe shape from the scans of the characterizers have been published (2-5).
1.3 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.

General Information

• Status: Historical
• Publication Date: 09-Jun-1996
• Technical Committee: E42 - Surface Analysis
• Drafting Committee: E42.14 - STM/AFM

Relations

• Replaced By: ASTM E1813-96(2002) - Standard Practice for Measuring and Reporting Probe Tip Shape in Scanning Probe Microscopy
• Effective Date: 10-Jun-1996
• Referred By: ASTM E2382-04(2020) - Standard Guide to Scanner and Tip Related Artifacts in Scanning Tunneling Microscopy and Atomic Force Microscopy
• Effective Date: 10-Jun-1996

Standards Content (Sample)

NOTICE: This standard has either been superseded and replaced by a new version or discontinued.
Contact ASTM International (www.astm.org) for the latest information.
e1
Designation: E 1813 – 96
Standard Practice for
Measuring and Reporting Probe Tip Shape in Scanning
Probe Microscopy
This standard is issued under the fixed designation E 1813; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
e NOTE—Editorial changes were made in July 1998.
INTRODUCTION
An image produced by a stylus scanning in close proximity to a surface is usually not an exact
replica of the surface. The data are subject to a type of distortion called dilation. The amount of
dilation depends on the shape and the orientation of the probe as well as the surface topography (1).
Analysis of the scanned probe images thus requires knowledge of the probe shape and orientation.
1. Scope
1.1 This practice covers scanning probe microscopy and
describes the parameters needed for probe shape and orienta-
tion.
1.2 This practice also describes a method for measuring the
shape and size of a probe tip to be used in scanning probe
microscopy. The method employs special sample shapes,
known as probe characterizers, which can be scanned with a
probe microscope to determine the dimensions of the probe.
Mathematical techniques to extract the probe shape from the
scans of the characterizers have been published (2-5).
FIG. 1 Probe Tip Characterization
1.3 This standard does not purport to address all of the
safety concerns, if any, associated with its use. It is the
3.1.2 characterized length—the region of the probe whose
responsibility of the user of this standard to establish appro-
shape has been measured with a probe characterizer (see Fig.
priate safety and health practices and determine the applica-
1).
bility of regulatory limitations prior to use.
3.1.3 concave probe—a probe that is not convex.
3.1.4 convex probe—the probe is convex if for any two
2. Referenced Documents
points in the probe, the straight line between the points lies in
2.1 ASTM Standards:
the probe.
F 1438 Test Method for Determination of Surface Rough-
3.1.4.1 Discussion—Conical and cylindrical probes are con-
ness by Scanning Tunneling Microscopy for Gas Distribu-
vex, while flared probes are not. Minor imperfections in the
tion System Components
probe, caused for instance by roughness of the probe surface,
should not be considered in determining whether a probe is
3. Terminology
convex.
3.1 Definitions:
3.1.5 dilation—the dilation of a set A by a set B is defined
3.1.1 active length—length of the region of the probe tip
as follows:
that could come into contact with the sample during a scan, and
A 1 B 5 ł~A 1 b!
is set by the height of the tallest feature encountered, and it
b{B (1)
should be less than the probe length (see Fig. 1).
The image I produced by a probe tip T scanning a surface S
is I = S +(−T) (6). This is the surface obtained if an inverted
image of the tip is placed at all points on the surface. The
This practice is under the jurisdiction of ASTM Committee E-42 on Surface
Analysis and is the direct responsibility of Subcommittee E42.14 on STM/ATM.
envelope produced by these inverted tip images is the image of
Current edition approved June 10, 1996. Published August 1996.
the surface (3).
The boldface numbers in parentheses refer to the list of references at the end of
3.1.6 erosion—the erosion of a set A by a set B is defined as
this document.
Annual Book of ASTM Standards, Vol 10.05. follows:
Copyright © ASTM, 100 Barr Harbor Drive, West Conshohocken, PA 19428-2959, United States.
E 1813
A 2 B 5 ø ~A 2 b!.
b{B (2)
An upper bound for the surface S is I −(−T), where I is the
image and − T is an inverted image of the probe tip (5).
3.1.7 feedback-induced distortion—distortion of a scan
trace arising from the inability of the probe microscope
feedback to maintain close proximity between the tip and
surface, which can be caused by scanning too quickly and
changes with scan speed and scan direction.
3.1.8 flexing-induced distortion—distortion of a scan trace
arising from flexing of the probe or shank during scanning.
3.1.9 probe apex—end of the probe tip, which is farthest
from the shank.
3.1.9.1 Discussion—For some shapes, the position of the
apex is somewhat arbitrary. The apex position coincides with
the origin of the coordinate system used to describe the probe.
3.1.10 probe characterizer—a structure designed to allow
extraction of the probe tip shape from a scan of the character-
izer.
3.1.11 probe flank—side of the probe in the region between
the apex and the shank.
3.1.12 probe length L —distance between the apex and the
t
shank (see Fig. 1).
3.1.13 probe shank—stiff structure supporting the probe tip.
3.1.14 probe stiffness—resistance of the probe from flexing
caused by lateral forces, expressed as a force constant (N/m)
describing the lateral flexing of the probe under an impressed
FIG. 2 Probe Tip Coordinates
force.
3.1.15 reconstruction—an estimate of the surface topogra-
phy determined by eroding the image with the probe tip shape.
3.1.15.1 Discussion—The closeness of the approximation
depends on both probe shape and surface topography. Regions
in which the estimate is not close are known as unreconstruc-
table regions or dead zones.
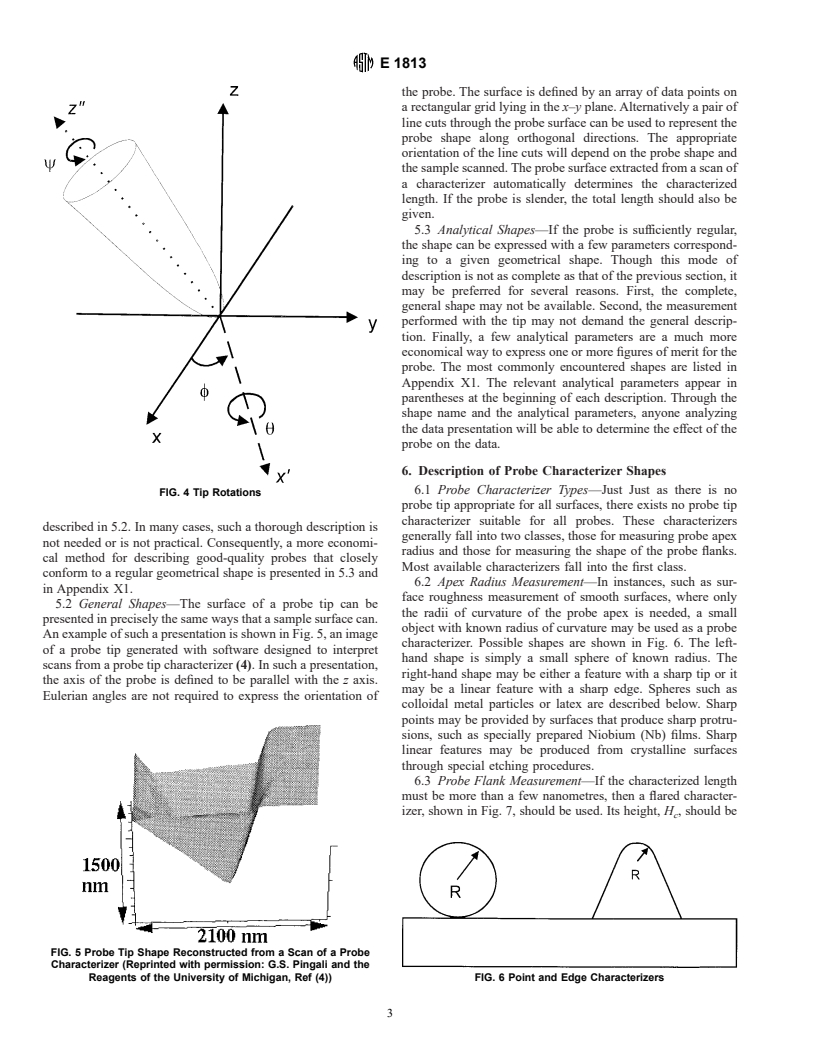
4. Coordinate System
4.1 The coordinate system used to describe the probe shape
is shown in Fig. 2 and Fig. 3. It is a three-dimensional,
right-handed, Cartesian system with mutually orthogonal axes
x, y and z. Distance along the axes is measured in nanometers
(nm) or micrometres (μm). In many cases, these axes will be
parallel to the corresponding axes used for the sample. The z
axis is chosen to be parallel to the axis of the probe. If the
probe is mounted on a cantilever, the orientation of the x and y
axes relative to the cantilever may be relevant because these
cantilevers are often tilted.
4.2 If the probe axis is tilted relative to the sample, Eulerian
angles should be used to express the orientation of the probe.
These angles are shown in Fig. 4. They may be expressed in
degrees. The order in which the rotations are applied is
FIG. 3 Coordinates Relative to Cantilever Orientation
important. The first is about the z axis through the angle f. The
second is about the x8 axis through the angle u. The final
5. Description of Probe Shapes
rotation is about the z9 axis through the angle c. The positive
sense of each rotation is determined by the right-hand screw 5.1 Probe tips usually have shapes that approximate regular
rule. Example: In a typical scanning force microscope, the geometrical solids, such as cones or cylinders. Because of
cantilever is tilted 10°. If the cantilever is oriented parallel to imperfections in manufacture or erosion during use, however,
the y axis before being tilted, then the orientation would be data are often collected with probes that are somewhat irregu-
u = −10°, f = 0° and c = 0°. lar. The most precise way to describe a probe is the method
E 1813
the probe. The surface is defined by an array of data points on
a rectangular grid lying in the x–y plane. Alternatively a pair of
line cuts through the probe surface can be used to represent the
probe shape along orthogonal directions. The appropriate
orientation of the line cuts will depend on the probe shape and
the sample scanned. The probe surface extracted from a scan of
a characterizer automatically determines the characterized
length. If the probe is slender, the total length should also be
given.
5.3 Analytical Shapes—If the probe is sufficiently regular,
the shape can be expressed with a few parameters correspond-
ing to a given geometrical shape. Though this mode of
description is not as complete as that of the previous section, it
may be preferred for several reasons. First, the complete,
general shape may not be available. Second, the measurement
performed with the tip may not demand the general descrip-
tion. Finally, a few analytical parameters are a much more
economical way to express one or more figures of merit for the
probe. The most commonly encountered shapes are listed in
Appendix X1. The relevant analytical parameters appear in
parentheses at the beginning of each description. Through the
shape name and the analytical parameters, anyone analyzing
the data presentation will be able to determine the effect of the
probe on the data.
6. Description of Probe Characterizer Shapes
6.1 Probe Characterizer Types—Just Just as there is no
FIG. 4 Tip Rotations
probe tip appropriate for all surfaces, there exists no probe tip
characterizer suitable for all probes. These characterizers
described in 5.2. In many cases, such a thorough description is
generally fall into two classes, those for measuring probe apex
not needed or is not practical. Consequently, a more economi-
radius and those for measuring the shape of the probe flanks.
cal method for describing good-quality probes that closely
Most available characterizers fall into the first class.
conform to a regular geometrical shape is presented in 5.3 and
6.2 Apex Radius Measurement—In instances, such as sur-
in Appendix X1.
face roughness measurement of smooth surfaces, where only
5.2 General Shapes—The surface of a probe tip can be
the radii of curvature of the probe apex is needed, a small
presented in precisely the same ways that a sample surface can.
object with known radius of curvature may be used as a probe
An example of such a presentation is shown in Fig. 5, an image
characterizer. Possible shapes are shown in Fig. 6. The left-
of a probe tip generated with software designed to interpret
hand shape is simply a small sphere of known radius. The
scans from a probe tip characterizer (4). In such a presentation,
right-hand shape may be either a feature with a sharp tip or it
the axis of the probe is defined to be parallel with the z axis.
may be a linear feature with a sharp edge. Spheres such as
Eulerian angles are not required to express the orientation of
colloidal metal particles or latex are described below. Sharp
points may be provided by surfaces that produce sharp protru-
sions, such as specially prepared Niobium (Nb) films. Sharp
linear features may be produced from crystalline surfaces
through special etching procedures.
6.3 Probe Flank Measurement—If the characterized length
must be more than a few nanometres, then a flared character-
izer, shown in Fig. 7, should be used. Its height, H , should be
c
FIG. 5 Probe Tip Shape Reconstructed from a Scan of a Probe
Characterizer (Reprinted with permission: G.S. Pingali and the
Reagents of the University of Michigan, Ref (4)) FIG. 6 Point and Edge Characterizers
E 1813
FIG. 7 Flared Probe Tip Characterizer
greater than the height of the tallest object to be scanned. When
the characterizer is scanned with the probe, the image will
contain probe tip images, which can be extracted with suitable
software. These flared features may be either one-dimensional
linear structures or two-dimensional plateaus.
6.4 Embodiments of Probe Characterizers:
6.4.1 Gold Colloid—Colloidal gold particles have multiple
uses as SPM imaging standard because they are incompress-
ible, stable monodispersive, and spherical. The particles are
available with three different diameters: 5.72 nm, 14.33 nm,
and 27.96 nm. Users can choose different sizes depending on
their applications. The particles can be absorbed on a substrate
(such as mica) along with biomolecules. The uniform spherical
shape of gold particles will give useful information about the
nano-geometry of the probe tip (6). Fig. 8 shows an AFM
image of gold colloids in distilled/deionized water and ad-
sorbed on to treated mica surface. All three sized particles are
present in the 1 by 1-μm scanned area. Image distortion due to
tip artifacts are present as well.
6.4.2 Strontium Titanate Crystal (SrTiO )—A high-
temperature-treated (305) surface of SrTiO results in a surface
with alternating (101) and (103) crystal planes and thus form
FIG. 8 Colloidal Gold Probe Characterizer (Reprinted with
large terraces. As shown in Fig. 9, the surface was character-
permission: A.T. Giberson, Ref (6))
ized by transmission electron microscopy (TEM) and revealed
the terraces with defined inclinations with respect to the surface
plan (305) of +14° and −11.6°, respectively. Reference (7) can
characterized using a field-emission SEM (FESEM) and found
be used to characterize the radius of a probe apex. Fig. 10
to be composed of very sharp pyramidal features. These
shows a series of profiles recorded with different commercial
features are sharp enough that AFM images of this surface
probes. The topmost profile demonstrates a Si N probe that
3 4
correspond to images of tip, instead of the thin film surface.
has a sharp probe apex, while Profile 2 and 3 reveal a truncated
Fig. 11 shows an AFM image of the Nb thin film. If the probe
probe apex of other Si N tips. Both an Si tip and e-beam-
3 4
apex of the AFM tip is assumed to be spherical, it is possible
deposited tip have a rounded probe apex as shown in the rest
to determine the radius of the probe apex from a cross section
of the profiles.
of the AFM image. The radius of the probe apex can be
6.4.3 Polycrystalline Nb Film—An Nb thin film (8,9) de-
calculated to be as follows:
posited on a silicon wafer by an electron-beam evaporation
2 2
method has a dense columnar microstructure. The surface was R 5 ~h 1 ~w/2! !/2h (3)
E 1813
FIG. 9 Transmission Electron Microscopy (TEM) Image of a (010) Cross Section Through a SrTiO Crystal (Reprinted with permission:
M. Moller, Ref (7))
FIG. 11 AFM Image of an e-beam-Evaporated Nb Thin Film
FIG. 10 Two-dimensional Profiles Obtained with a Variety of
(Reprinted with permission: K.L. Westra, Ref (8))
Probe Tips (Reprinted with permission: M. Moller, Ref (7))
They are shown in Figs. 13 and 14. Fig. 13 is a linear sawtooth
where
structure with edge radii of approximately 5 nm. Fig. 14 is a
w = width of the feature, and
flared structure with edge radii less than 10 nm and a height of
h = height (see Fig. 12).
3to4μm.
6.4.4 Polystyrene Latex Particles—The polystyrene latex
7. Significance and Use
particles (10) have uniform spherical shape with size distribu-
tions ranging from 60 to 500 nm. Using appropriate tip shape 7.1 The shape and orientation of the probe tip determines
extraction software, the geometry of the probe shape can be which information can be reliably extracted from a scan. This
extracted as with the colloidal gold. The latex particles must applies to all typ
...