ASTM E1049-85(2005)
(Practice)Standard Practices for Cycle Counting in Fatigue Analysis
Standard Practices for Cycle Counting in Fatigue Analysis
SIGNIFICANCE AND USE
Cycle counting is used to summarize (often lengthy) irregular load-versus-time histories by providing the number of times cycles of various sizes occur. The definition of a cycle varies with the method of cycle counting. These practices cover the procedures used to obtain cycle counts by various methods, including level-crossing counting, peak counting, simple-range counting, range-pair counting, and rainflow counting. Cycle counts can be made for time histories of force, stress, strain, torque, acceleration, deflection, or other loading parameters of interest.
SCOPE
1.1 These practices are a compilation of acceptable procedures for cycle-counting methods employed in fatigue analysis. This standard does not intend to recommend a particular method.
1.2 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E1049 – 85 (Reapproved 2005)
Standard Practices for
Cycle Counting in Fatigue Analysis
This standard is issued under the fixed designation E1049; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision. A number in parentheses indicates the year of last reapproval. A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope 3.1.3.1 Discussion—For purposes related to cycle counting,
a mean crossing may be defined as a crossing of the reference
1.1 These practices are a compilation of acceptable proce-
load level.
duresforcycle-countingmethodsemployedinfatigueanalysis.
3.1.4 mean load, P —in fatigue loading, the algebraic
This standard does not intend to recommend a particular m
average of the maximum and minimum loads in constant
method.
amplitude loading, or of individual cycles in spectrum loading,
1.2 This standard does not purport to address all of the
safety concerns, if any, associated with its use. It is the P 5 ~P 1 P !/2 (1)
m max min
responsibility of the user of this standard to establish appro-
priate safety and health practices and determine the applica-
ortheintegralaverageoftheinstantaneousloadvaluesorthe
bility of regulatory limitations prior to use.
algebraic average of the peak and valley loads of a spectrum
loading history.
2. Referenced Documents
3.1.5 peak—in fatigue loading, the point at which the first
2.1 ASTM Standards:
derivative of the load-time history changes from a positive to
E912 Definitions of Terms Relating to Fatigue Loading
a negative sign; the point of maximum load in constant
amplitude loading (see Fig. 1).
3. Terminology
3.1.6 range—in fatigue loading, the algebraic difference
3.1 Definitions:
between successive valley and peak loads (positive range or
3.1.1 constant amplitude loading—in fatigue loading,a
increasing load range), or between successive peak and valley
loading in which all of the peak loads are equal and all of the
loads (negative range or decreasing load range); see Fig. 1.
valley loads are equal.
NOTE 2—In spectrum loading, range may have a different definition,
3.1.2 cycle—in fatigue loading, under constant amplitude
depending on the counting method used; for example, “overall range” is
loading, the load variation from the minimum to the maximum
defined by the algebraic difference between the largest peak and the
and then to the minimum load.
smallest valley of a given load-time history.
NOTE 1—In spectrum loading, definition of cycle varies with the
3.1.6.1 Discussion—In cycle counting by various methods,
counting method used.
it is common to employ ranges between valley and peak loads,
3.1.3 mean crossings—in fatigue loading, the number of or between peak and valley loads, which are not necessarily
times that the load-time history crosses the mean-load level
successive events. In these practices, the definition of the word
with a positive slope (or a negative slope, or both, as specified) “range” is broadened so that events of this type are also
during a given length of the history (see Fig. 1).
included.
3.1.7 reversal—in fatigue loading, the point at which the
first derivative of the load-time history changes sign (see Fig.
ThesepracticesareunderthejurisdictionofASTMCommitteeE0-8onFatigue
1).
and Fracture and are the direct responsibility of Subcommittee E08.04 on Structural
Applications.
NOTE 3—In constant amplitude loading, a cycle is equal to two
Current edition approved June 1, 2005. Published June 2005. Originally
reversals.
approvedin1985.Lastpreviouseditionapprovedin1997asE1049–85(1997).DOI:
10.1520/E1049-85R05.
3.1.8 spectrum loading—in fatigue loading, a loading in
For referenced ASTM standards, visit the ASTM website, www.astm.org, or
which all of the peak loads are not equal or all of the valley
contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
loadsarenotequal,orboth.(Alsoknownasvariableamplitude
Standards volume information, refer to the standard’s Document Summary page on
the ASTM website.
loading or irregular loading.)
Withdrawn.Thelastpreviouseditionofthishistoricalstandardisreferencedon
www.astm.org.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
E1049 – 85 (2005)
FIG. 1 Basic Fatigue Loading Parameters
3.1.9 valley—in fatigue loading, the point at which the first counting. A second method is to make no counts at the
derivative of the load-time history changes from a negative to reference load and to specify that only one count be made
a positive sign (also known as trough); the point of minimum between successive crossings of a secondary lower level
load in constant amplitude loading (see Fig. 1). associated with each level above the reference load, or a
3.2 Definitions of Terms Specific to This Standard: secondary higher level associated with each level below the
3.2.1 load—used in these practices to denote force, stress,
reference load. Fig. 2(b) illustrates this second method. A
strain, torque, acceleration, deflection, or other parameters of variation of the second method is to use the same secondary
interest.
level for all counting levels above the reference load, and
3.2.2 reference load—for spectrum loading, used in these another for all levels below the reference load. In this case the
practices to denote the loading level that represents a steady-
levels are generally not evenly spaced.
state condition upon which load variations are superimposed.
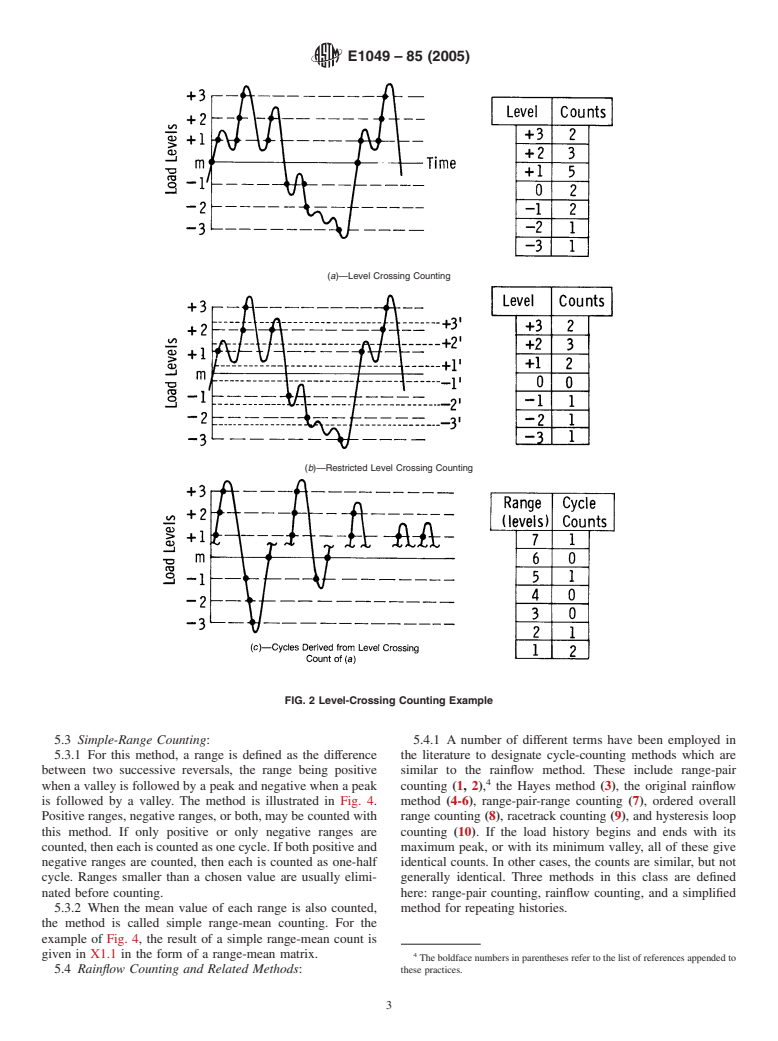
5.1.3 The most damaging cycle count for fatigue analysis is
The reference load may be identical to the mean load of the
derived from the level-crossing count by first constructing the
history, but this is not required.
largest possible cycle, followed by the second largest, etc.,
3.3 For other definitions of terms used in these practices
until all level crossings are used. Reversal points are assumed
refer to Definitions E912.
to occur halfway between levels. This process is illustrated by
Fig. 2(c). Note that once this most damaging cycle count is
4. Significance and Use
obtained, the cycles could be applied in any desired order, and
4.1 Cycle counting is used to summarize (often lengthy)
this order could have a secondary effect on the amount of
irregularload-versus-timehistoriesbyprovidingthenumberof
damage. Other methods of deriving a cycle count from the
times cycles of various sizes occur. The definition of a cycle
level-crossings count could be used.
varieswiththemethodofcyclecounting.Thesepracticescover
5.2 Peak Counting:
the procedures used to obtain cycle counts by various methods,
5.2.1 Peak counting identifies the occurrence of a relative
including level-crossing counting, peak counting, simple-range
maximum or minimum load value. Peaks above the reference
counting, range-pair counting, and rainflow counting. Cycle
load level are counted, and valleys below the reference load
counts can be made for time histories of force, stress, strain,
level are counted, as shown in Fig. 3(a). Results for peaks and
torque, acceleration, deflection, or other loading parameters of
valleys are usually reported separately. A variation of this
interest.
method is to count all peaks and valleys without regard to the
reference load.
5. Procedures for Cycle Counting
5.2.2 To eliminate small amplitude loadings, mean-crossing
5.1 Level-Crossing Counting:
peak counting is often used. Instead of counting all peaks and
5.1.1 Results of a level-crossing count are shown in Fig.
valleys, only the largest peak or valley between two successive
2(a). One count is recorded each time the positive sloped
mean crossings is counted as shown in Fig. 3(b).
portion of the load exceeds a preset level above the reference
load, and each time the negative sloped portion of the load 5.2.3 The most damaging cycle count for fatigue analysis is
exceeds a preset level below the reference load. Reference load derived from the peak count by first constructing the largest
crossings are counted on the positive sloped portion of the possible cycle, using the highest peak and lowest valley,
loading history. It makes no difference whether positive or followed by the second largest cycle, etc., until all peak counts
negative slope crossings are counted. The distinction is made are used.This process is illustrated by Fig. 3(c). Note that once
only to reduce the total number of events by a factor of two. thismostdamagingcyclecountisobtained,thecyclescouldbe
5.1.2 In practice, restrictions on the level-crossing counts applied in any desired order, and this order could have a
are often specified to eliminate small amplitude variations secondary effect on the amount of damage. Alternate methods
which can give rise to a large number of counts. This may be of deriving a cycle count, such as randomly selecting pairs of
accomplished by filtering small load excursions prior to cycle peaks and valleys, are sometimes used.
E1049 – 85 (2005)
(a)—Level Crossing Counting
(b)—Restricted Level Crossing Counting
FIG. 2 Level-Crossing Counting Example
5.3 Simple-Range Counting: 5.4.1 A number of different terms have been employed in
5.3.1 For this method, a range is defined as the difference the literature to designate cycle-counting methods which are
between two successive reversals, the range being positive similar to the rainflow method. These include range-pair
when a valley is followed by a peak and negative when a peak counting (1, 2), the Hayes method (3), the original rainflow
is followed by a valley. The method is illustrated in Fig. 4. method (4-6), range-pair-range counting (7), ordered overall
Positive ranges, negative ranges, or both, may be counted with range counting (8), racetrack counting (9), and hysteresis loop
this method. If only positive or only negative ranges are counting (10). If the load history begins and ends with its
counted, then each is counted as one cycle. If both positive and maximum peak, or with its minimum valley, all of these give
negative ranges are counted, then each is counted as one-half identical counts. In other cases, the counts are similar, but not
cycle. Ranges smaller than a chosen value are usually elimi- generally identical. Three methods in this class are defined
nated before counting. here: range-pair counting, rainflow counting, and a simplified
5.3.2 When the mean value of each range is also counted, method for repeating histories.
the method is called simple range-mean counting. For the
example of Fig. 4, the result of a simple range-mean count is
given in X1.1 in the form of a range-mean matrix.
The boldface numbers in parentheses refer to the list of references appended to
5.4 Rainflow Counting and Related Methods: these practices.
E1049 – 85 (2005)
(a)—Peak Counting
(b)—Mean Crossing Peak Counting
(c)—Cycles Derived from Peak Count of (a)
FIG. 3 Peak Counting Example
5.4.2 The various methods similar to the rainflow method (3) Compare the absolute values of ranges X and Y.
may be used to obtain cycles and the mean value of each cycle; (a)If X < Y, go to Step 1.
they are referred to as two-parameter methods.When the mean (b)If X$ Y, go to Step 4.
value is ignored, they are one-parameter methods, as are (4) Count range Y as one cycle and discard the peak and
simple-range counting, peak counting, etc. valley of Y; go to Step 2.
5.4.3 Range-Pair Counting—The range-paired method (5) The remaining cycles, if any, are counted by starting at
counts a range as a cycle if it can be paired with a subsequent the end of the sequence and counting backwards. If a single
loading in the opposite direction. Rules for this method are as range remains, it may be counted as a half or full cycle.
follows: 5.4.3.2 The load history in Fig. 4 is replotted as Fig. 5(a)
5.4.3.1 Let X denote range under consideration; and Y, and is used to illustrate the process. Details of the cycle
previous range adjacent to X. counting are as follows:
(1) Read next peak or valley. If out of data, go to Step 5. (1) Y =|A-B|; X =|B-C|; andX>Y. Count |A-B|asone
(2) If there are less than three points, go to Step 1. Form cycle and discard points A and B. (See Fig. 5(b). Note that a
ranges X and Y using the three most recent peaks and valleys cycle is formed by pairing range A-B and a portion of range
that have not been discarded. B-C.)
E1049 – 85 (2005)
FIG. 4 Simple Range Counting Example—Both Positive and Negative Ranges Counted
(2) Y = |C-D|; X = |D-E|; andX
(3) Y = |D-E|; X = |E-F|; andX
second point in range Y; and go to Step 2.
(4) Y = |E-F|; X = |F-G|; andX>Y. Count |E-F|asone
cycle and discard points E and F. (See Fig. 5(c).) (6) Count each range that has not been previously counted
(5) Y = |C-D|; X = |D-G|; andX>Y. Count |C-D| as one as one-half cycle.
cycle and discard points C and D. (See Fig. 5(d).)
5.4.4.2 The load history of Fig. 4 is replotted as Fig. 6(a)
(6) Y = |G-H|; X = |H-I|; andX
and is used to illustrate the process. Details of the cycle
count backwards.
counting are as follows:
(7) Y = |H-I|; X = |G-H|; andX>Y. Count |H-I|asone
(1) S = A; Y = |A-B|; X = |B-C|;X>Y.Y contains S, that is,
cycle and discard points H and I. (See Fig. 5(e).)
point A. Count |A-B| as one-half cycle and discard point A;
(8) End of counting. See the table in Fig. 5 for a summary
S=B. (See Fig. 6(b).)
of the cycles counted in this example, and see Appendix X1.2
(2) Y = |B-C|; X = |C-D|;X>Y.Y contains S, that is, point
for this cycle count in the form of a range-mean matrix.
B. Count| B-C| as one-half cycle and discard point B; S=C.
5.4.4 Rainflow Counting:
(See Fig. 6(c).)
5.4.4.1 Rules for this method are as follows: let X denote
(3) Y = |C-D|; X = |D-E|;X
rangeunderconsideration; Y,previousrangeadjacentto X;and
(4) Y = |D-E|; X = |E-F|;X
S, starting point in the history.
(5) Y = |E-F|; X = |F-G|;X>Y. Count |E-F| as one cycle
(1) Read next peak or valley. If out of data, go to Step 6.
and discard points E and F. (See Fig. 6(d). Note that a cycle is
(2) If there are less than three points, go to Step 1. Form
formed by pairing range E-F and a portion of range F-G.)
ranges X and Y using the three most recent peaks and valleys
(6) Y = |C-D|; X = |D-G|;X>Y; Y contains S, that is, point
that have not been discarded.
C. Count |C-D| as one-half cycle and discard point C.S=D.
(3) Compare the absolute values of ranges X and Y.
(See Fig. 6(e).)
(a)IfX
(7) Y = |D-G|; X = |G-
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.