ASTM F83-71(2002)

Standard Practice for Definition and Determination of Thermionic Constants of Electron Emitters

ABSTRACT
This practice covers the definition and interpretation of the commonly used thermionic constants of electron emitters with appended standard methods of measurement. Cathode materials shall alternatively be evaluated by relating the temperature-limited emission to fundamental properties of the emitter, particularly the work function. Comparisons are made between emitters using the thermionic constants such as the work function, emission constant, and the temperature dependence of the work function. These thermionic constants are geometry and field effects-independent, but exhibit variations under different conditions. The pertinent equations the Richardson-Dushman equation of electron emission to evaluate the effective work function, which in turn, shall be used to find the Richardson work function and the true work function. Sample computations are also detailed.
SCOPE
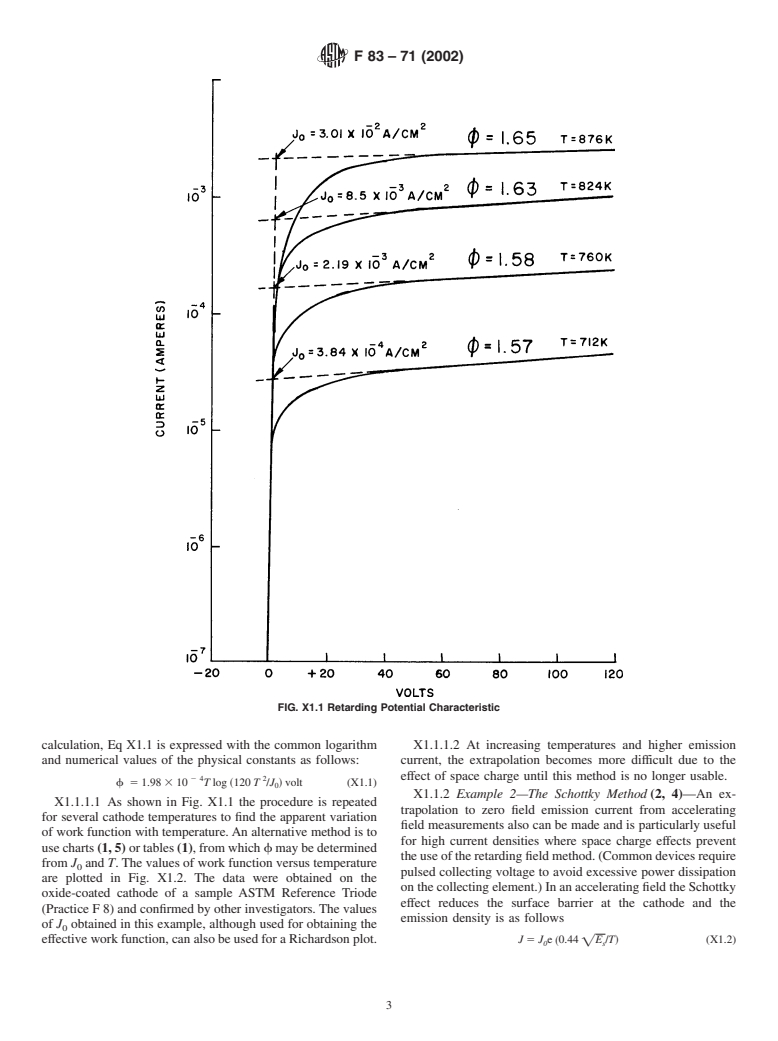
1.1 This practice covers the definition and interpretation of the commonly used thermionic constants of electron emitters  (1, 2, 3), with appended standard methods of measurement.

General Information

• Status: Historical
• Publication Date: 30-Mar-1971
• ICS: 01.040.31 - Electronics (Vocabularies)
• ICS: 31.100 - Electronic tubes
• Technical Committee: F01 - Electronics
• Drafting Committee: F01.03 - Metallic Materials, Wire Bonding, and Flip Chip

Relations

• Replaces: ASTM F83-71(1996)e1 - Standard Practice for Definition and Determination of Thermionic Constants of Electron Emitters
• Effective Date: 31-Mar-1971
• Replaced By: ASTM F83-71(2009) - Standard Practice for Definition and Determination of Thermionic Constants of Electron Emitters
• Effective Date: 01-May-2009

Standards Content (Sample)

NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: F 83 – 71 (Reapproved 2002)
Standard Practice for
Definition and Determination of Thermionic Constants of
1
Electron Emitters
ThisstandardisissuedunderthefixeddesignationF83;thenumberimmediatelyfollowingthedesignationindicatestheyearoforiginal
adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.Asuperscript
epsilon (e) indicates an editorial change since the last revision or reapproval.
INTRODUCTION
Cathode materials are often evaluated by an emission test which in some ways measures the
temperature-limited emission. A more basic approach to this problem is to relate the emission to
fundamental properties of the emitter, in particular, the work function. Comparisons are conveniently
made between emitters using the thermionic constants, that is, the work function, the emission
constant, and the temperature dependence of the work function. These quantities are independent of
geometry and field effects when properly measured. Although referred to as “constants” these
quantities show variations under different conditions. Considerable confusion exists over the
definition, interpretation, and usage of these terms and, hence, there is a need for at least a general
agreement on nomenclature.
1. Scope
where:
2
J = emission current density in A/cm measured under
1.1 This practice covers the definition and interpretation of
specified field conditions except zero field.
the commonly used thermionic constants of electron emitters
2
2
(J = emission current density in A/cm measured un-
(1, 2, 3), with appended standard methods of measurement.
0
der zero field conditions.)
2. Referenced Documents
A = the theoretical emission constant, which is calculated
from fundamental physical constants, with its value
2.1 ASTM Standards:
2 2
generally taken as 120 A/cm ·K . A more exact calcu-
F 8 Practice for Testing Electron Tube Materials Using
3
lation (3) gives 120.17 which is used in determining
Reference Triodes
the effective work function.
3. Terminology T = cathode temperature, K.
e = electronic charge, C.
3.1 Definitions:
e = natural logarithmic base.
3.1.1 effective work function, f—the work function ob-
k = Boltzmann’s constant.
tained by the direct substitution of experimentally determined
f = work function, V.
values of emission current density and temperature into the
The form of Eq 1 is a simplified form of the emission
Richardson-Dushman equation of electron emission of the
equationwhichassumeszeroreflectioncoefficientforelectrons
form:
with energy normally sufficient for emission at the emitter
2 2ef/kT
J 5 AT e (1)
surface. The effective work function is an empirical quantity
and represents an average of the true work function, giving the
For direct calculation of the work function, this is conve-
maximum information obtainable from a single measurement
niently put in the form:
of the thermionic emission.
2
f5~kT/e! ln ~AT /J! (2)
3.1.2 Richardson work function, f —the work function
0
usually obtained graphically from a Richardson plot, which is
2
1
a plot of ln (J/T ) versus l/T using data of emission measure-
This practice is under the jurisdiction ofASTM Committee F01 on Electronics
and is the direct responsibility of Subcommittee F01.03 on Metallic Materials.
ments at various temperatures. It is the work function obtained
Current edition approved March 31, 1971. Published May 1971. Originally
from Eq 1, with the value of A determined graphically, instead
published as F 83 – 67 T. Last previous edition F 83 – 67 T.
2 of using the theoretical value. For better visualization of the
The boldface numbers in parentheses refer to references at the end of this
Richardson plot, Eq 1 may be put in the form:
practice.
3
Discontinued, see 1971 Annual Book of ASTM Standards, Part 43.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
1

---------------------- Page: 1 ----------------------
F 83 – 71 (2002)
2
representing the value at 0 K. The effective work function at
ln ~J/T ! 5 lnA2~e/kT!f (3)
0
temperature T is then equal to f + aT. Substituting this into
0
It can be seen (Fig. X1.4) that the Richardson work function
the equation gives:
f is obtained from the slope of the graph, and the emission
0
2 2~e/kT!~f
2 01aT!
J 5 AT e (4)
constant A from the intercept (l/T = 0) on the ln (J/T ) axis.
The Richardson work function is also an empirical quantity. Its
which can be put in the form:
value is found with reasonable accuracy from the graph.
2ea/k 2 2ef
0/kT
J5~Ae !T e (5)
However, large errors in the value of Amay be expected (4).
It can be seen from Eq 5 that a Richardson plot slope would
Considering only one factor, a slight inaccuracy in the mea-
determine f and a value of the emission constant e−ea/ktimes
surement of t
...