ASTM E158-86(1996)e1
(Practice)Standard Practice for Fundamental Calculations to Convert Intensities into Concentrations in Optical Emission Spectrochemical Analysis (Withdrawn 2004)
Standard Practice for Fundamental Calculations to Convert Intensities into Concentrations in Optical Emission Spectrochemical Analysis (Withdrawn 2004)
SCOPE
1.1 This practice covers fundamental forms of plots, used to convert measured intensities into concentrations in both photographic and direct reading analysis. It includes equations suitable for use with calculators or computers for such conversions, and methods for making background corrections and corrections for interferences from other elements.
1.2 A previous issue of this practice attempted to treat optical emission and X-ray fluorescence as one field, employing similar calculations to convert measured radiation intensities into concentrations. In fact, quite different procedures are used in the two fields. This practice confines itself to optical emission spectrochemical analysis. A separate practice will be devoted to calculations in X-ray fluorescence spectroscopy.
1.3 This practice is related to but should be distinguished from:
1.3.1 Practice E116, which describes procedures for converting either transmittance or optical density of lines on a photographic emulsion into intensities or relative intensities. This step is required in photographic analysis before the present practice can be applied.
1.3.2 Practice E305, which describes the procedures for fitting a curve to a group of plotted points, and for standardizing the equipment, in order to obtain optimum accuracy, guided by sound statistical practice.
1.3.3 Practice E876 discusses the statistical treatment commonly applied to spectrochemical data, such as calculating the standard deviation and the relative standard deviation.
1.4 This practice includes the following sections: Section Referenced Documents 2 Terminology 3 Significance and Use 4 Fundamental Theory 5 Plotting Analytical Curves with a Constant Internal Standard 6 Plotting Analytical Curves with a Variable Internal Standard 7 Background Correction 8 Concentration Calculations 9 Corrections for Interferences from Other Elements 10
1.5 This standard does not purport to address all of the safety concerns, if any, associated with its use. It is the responsibility of the user of this standard to establish appropriate safety and health practices and determine the applicability of regulatory limitations prior to use.
WITHDRAWN RATIONALE
This practice covers fundamental forms of plots, used to convert measured intensities into concentrations in both photographic and direct reading analysis. Formerly under the juridiction of Committee E01 on Analytical Chemistry for Metals, Ores and Related Materials, this practice was withdrawn in May 2004 because it does not reflect the current practice.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Please contact ASTM International (www.astm.org) for the latest information.
´1
Designation: E 158 – 86 (Reapproved 1996)
Standard Practice for
Fundamental Calculations to Convert Intensities into
Concentrations in Optical Emission Spectrochemical
Analysis
This standard is issued under the fixed designation E158; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
´ NOTE—Keywords were added editorially in June 1996.
1. Scope
Fundamental Theory 5
Plotting Analytical Curves with a Constant Internal Stan- 6
1.1 Thispracticecoversfundamentalformsofplots,usedto
dard
convert measured intensities into concentrations in both pho-
Plotting Analytical Curves with a Variable Internal Stan- 7
dard
tographic and direct reading analysis. It includes equations
Background Correction 8
suitable for use with calculators or computers for such conver-
Concentration Calculations 9
sions, and methods for making background corrections and
Corrections for Interferences from Other Elements 10
corrections for interferences from other elements.
1.5 This standard does not purport to address all of the
1.2 A previous issue of this practice attempted to treat
safety concerns, if any, associated with its use. It is the
optical emission and X-ray fluorescence as one field, employ-
responsibility of the user of this standard to establish appro-
ing similar calculations to convert measured radiation intensi-
priate safety and health practices and determine the applica-
ties into concentrations. In fact, quite different procedures are
bility of regulatory limitations prior to use.
used in the two fields. This practice confines itself to optical
emission spectrochemical analysis.Aseparate practice will be
2. Referenced Documents
devoted to calculations in X-ray fluorescence spectroscopy.
2.1 ASTM Standards:
1.3 This practice is related to but should be distinguished
E116 Practice for Photographic Photometry in Spectro-
from: 2
chemical Analysis
1.3.1 Practice E116E116, which describes procedures for
E135 Terminology Relating to Analytical Chemistry for
converting either transmittance or optical density of lines on a 2
Metals, Ores, and Related Materials
photographic emulsion into intensities or relative intensities.
E305 Practice for Establishing and Controlling Spectro-
This step is required in photographic analysis before the 2
chemical Analytical Curves
present practice can be applied.
E876 Practice for the Use of Statistics in the Evaluation of
1.3.2 Practice E305E305, which describes the procedures 3
Spectrometric Data
for fitting a curve to a group of plotted points, and for
standardizing the equipment, in order to obtain optimum 3. Terminology
accuracy, guided by sound statistical practice.
3.1 For definitions of terms used in this practice, refer to
1.3.3 Practice E876E876 discusses the statistical treatment
Terminology E135E135.
commonlyappliedtospectrochemicaldata,suchascalculating
the standard deviation and the relative standard deviation. 4. Significance and Use
1.4 This practice includes the following sections:
4.1 Overtheyears,manyworkershavedevelopedimproved
Section
methods for plotting the measured intensities obtained from
Referenced Documents 2
chemically analyzed specimens (“standards”), and for calcu-
Terminology 3
Significance and Use 4 latingconcentrationsofunknownsfromthe“analytical”curves
obtained. This practice describes the methods of plotting and
the calculation techniques which have been found to produce
This practice is under the jurisdiction of ASTM Committee E-1 on Analytical superior results.
Chemistry for Metals, Ores and Related Materials and is the direct responsibility of
Subcommittee E01.22 on Statistics and Quality Control.
Current edition approved Oct. 31, 1986. Published December 1986. Originally Annual Book of ASTM Standards, Vol 03.05.
published as E158–60T. Last previous edition E158–83. Annual Book of ASTM Standards, Vol 03.06.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Please contact ASTM International (www.astm.org) for the latest information.
´1
E 158 – 86 (1996)
5.2.1 Over the years, power supplies for sampling and
exciting materials have become much more stable, and expo-
sure variations have been reduced, but in general, the internal
standard procedure still produces better results than the use of
absolute intensities. Accordingly, the method is employed
almost universally.
6. Plotting Analytical Curves with a Constant Internal
FIG. 1 The Advantage of Using an Internal Standard
Standard
6.1 Log-Log, Linear, and Log-Linear Plots—Different plot-
ting methods produce analytical curves of widely different
appearance. Each has its own advantages. Fig. 2, Fig. 3, and
Fig. 4 illustrate the curves most commonly employed. The
characteristics of each are listed. It should be emphasized that
a knowledge of the theoretical shape of a curve can assist in
deciding how best to fit a curve to an array of plotted points.
FIG. 2 Log-Log Plot
5. Fundamental Theory
5.1 In optical emission spectrochemical analysis, there are
relatively few interferences from other elements, for materials
with spectra of normal complexity, provided that a spec-
trograph or spectrometer with adequate dispersion and resolu-
tion is used, and that analytical lines are selected carefully. In
general, the intensity of an analytical line is a function only of
FIG. 3 Linear Plot
the concentration of the element that produces it. Therefore, it
is common practice to employ an individual analytical curve
6.2 Theoretical Data—The theoretical data used to plot the
for each element in a matrix. Observed intensities are con-
curves are presented in Table 1. It is assumed that throughout
vertedintoconcentrationsdirectlyfromthiscurve,withoutany
the series of measurements the ratio of the intensity of the
correction for other elements. However, at times, it may be
background to the intensity of the internal standard line
desirable to apply corrections for background or for interfer-
remains constant, at 0.030.At low concentrations, the ratio of
ences from other elements, as discussed later in this practice.
theintensityoftheanalyticallinetotheintensityoftheinternal
5.2 Internal Standard Method—In the early days of quan-
standard line (I /I ) is assumed to vary in direct proportion to
titative optical emission spectrochemical analysis, Gerlach and a s
the concentration. At 0.01%, (Column 2), it is assumed to
Schweitzer found that when they measured the “blacknesses”
measure 0.100 (Column 3); therefore at 0.0032%, it will
of lines produced on photographic emulsion by a series of
measure 0.032, etc. The total signal is the sum of the intensity
chemically analyzed materials and plotted them against their
ratios of the background and line. Thus, at 0.01%, it is 0.130;
known concentrations, quite erratic results were obtained. A
at 0.0032%, it is 0.062, etc.The table first lists concentrations
single specimen gave different “blacknesses” when run repeat-
down to 0.0001%, where the line signal is 0.001, and the
edly.Thesevariationswereascribedtoerraticexcitationandto
background, 0.030. Then the table lists increasing concentra-
variations in illumination. If they measured a line of an
tions. At 0.32%, it is assumed that self-absorption is signifi-
“internal standard element” that had the same concentration in
cant, so that the line response is not as great as the increase in
all their materials, they could measure these exposure varia-
concentration. The data tabulated in Column 5 are explained
tions. Ratios determined by dividing the “blackness” of an
later in 6.5.1.
analytical line by the “blackness” of an internal standard line,
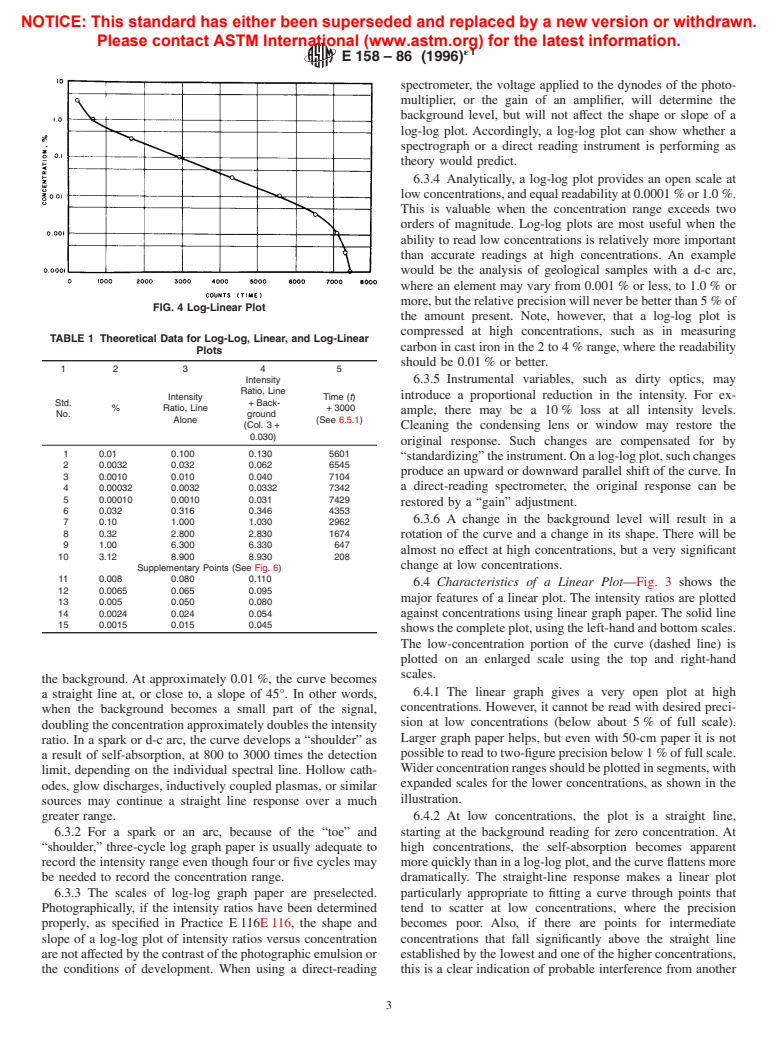
6.3 Characteristics of Log-Log Plots—Fig. 2 shows the
gave more repeatable results when the same material was
appearance and major features of a log-log plot. The intensity
burned repeatedly. Plots of “blackness” ratios versus concen-
ratiosofthetotalsignal(Column4,Table1)areplottedagainst
tration produced analytical curves with a better fit of points.
concentrations (Column 2), using log-log graph paper. In the
Fig.1illustratestheadvantagesinprecisionandfitofpointsto
illustration, intensity ratios are plotted vertically, since these
a curve obtained by the internal standard technique, when
are measured, and concentrations horizontally, since they are
applied to the determination of nickel in low-alloy steels.
known (at the time of plotting the curve). However, some
Curves plotted on linear graph paper are used for illustration.
workers prefer to reverse the scales.
6.3.1 Below the detection limit, the curve starts as a
horizontal line, corresponding to the spectral background. The
Gerlach, W., and Schweitzer, E., Foundations and Methods of Chemical
Analysis by the Emission Spectrum, Adam Hilger, Ltd., London, 1929. curverisesslowlyasthelinesignalcanbedistinguishedabove
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Please contact ASTM International (www.astm.org) for the latest information.
´1
E 158 – 86 (1996)
spectrometer, the voltage applied to the dynodes of the photo-
multiplier, or the gain of an amplifier, will determine the
background level, but will not affect the shape or slope of a
log-log plot. Accordingly, a log-log plot can show whether a
spectrograph or a direct reading instrument is performing as
theory would predict.
6.3.4 Analytically, a log-log plot provides an open scale at
lowconcentrations,andequalreadabilityat0.0001%or1.0%.
This is valuable when the concentration range exceeds two
orders of magnitude. Log-log plots are most useful when the
ability to read low concentrations is relatively more important
than accurate readings at high concentrations. An example
would be the analysis of geological samples with a d-c arc,
where an element may vary from 0.001% or less, to 1.0% or
more,buttherelativeprecisionwillneverbebetterthan5%of
FIG. 4 Log-Linear Plot
the amount present. Note, however, that a log-log plot is
compressed at high concentrations, such as in measuring
TABLE 1 Theoretical Data for Log-Log, Linear, and Log-Linear
carbon in cast iron in the 2 to 4% range, where the readability
Plots
should be 0.01% or better.
12 3 4 5
Intensity
6.3.5 Instrumental variables, such as dirty optics, may
Ratio, Line
introduce a proportional reduction in the intensity. For ex-
Intensity Time (t)
Std. + Back-
% Ratio, Line + 3000
ample, there may be a 10% loss at all intensity levels.
No. ground
Alone (See 6.5.1)
(Col. 3 +
Cleaning the condensing lens or window may restore the
0.030)
original response. Such changes are compensated for by
1 0.01 0.100 0.130 5601
“standardizing”theinstrument.Onalog-logplot,suchchanges
2 0.0032 0.032 0.062 6545
produce an upward or downward parallel shift of the curve. In
3 0.0010 0.010 0.040 7104
4 0.00032 0.0032 0.0332 7342 a direct-reading spectrometer, the original response can be
5 0.00010 0.0010 0.031 7429
restored by a “gain” adjustment.
6 0.032 0.316 0.346 4353
6.3.6 A change in the background level will result in a
7 0.10 1.000 1.030 2962
8 0.32 2.800 2.830 1674
rotation of the curve and a change in its shape. There will be
9 1.00 6.300 6.330 647
almost no effect at high concentrations, but a very significant
10 3.12 8.900 8.930 208
change at low concentrations.
Supplementary Points (See Fig. 6)
11 0.008 0.080 0.110
6.4 Characteristics of a Linear Plot—Fig. 3 shows the
12 0.0065 0.065 0.095
major features of a linear plot. The intensity ratios are plotted
13 0.005 0.050 0.080
14 0.0024 0.024 0.054 against concentrations using linear graph paper. The solid line
15 0.0015 0.015 0.045
showsthecompleteplot,usingtheleft-handandbottomscales.
The low-concentration portion of the curve (dashed line) is
plotted on an enlarged scale using the top and right-hand
scales.
the background. At approximately 0.01%, the curve becomes
6.4.1 The linear graph gives a very open plot at high
a straight line at, or close to, a slope of 45°. In other words,
concentrations. However, it cannot be read with desired preci-
when the background becomes a small part of the signal,
sion at low concentrations (below about 5% of full scale).
doublingtheconcentrationapproximatelydoublestheintensity
Larger graph paper helps, but even with 50-cm paper it is not
ratio. In a spark or d-c arc, the curve develops a “shoulder” as
possibletoreadtotwo-figureprecisionbelow1%offullscale.
a result of self-absorption, at 800 to 3000 times the detection
Widerconcentrationrangesshouldbeplottedinsegments,with
limit, depending on the individual spectral line. Hollow cath-
expanded scales for the lower concentrations, as shown in the
odes, glow discharges, inductively coupled plasmas, or similar
illustration.
sources may continue a straight line response over a much
greater range. 6.4.2 At low concentrations, the plot is a straight line,
6.3.2 For a spark or an arc, because of the “toe” and starting at the background reading for zero concentration. At
“shoulder,” three-cycle log graph paper is usually adequate to high concentrations, the self-absorption becomes apparent
record the intensity range even though four or five cycles may morequicklythaninalog-logplot,andthecurveflattensmore
be needed to record the concentration range. dramatically. The straight-line response makes a linear plot
6.3.3 The scales of log-log graph paper are preselected. particularly appropriate to fitting a curve through points that
Photographically, if the intensity ratios have been determined tend to scatter at low concentrations, where the precision
properly, as specified in Practice E116E116, the shape and becomes poor. Also, if there are points for intermediate
slope of a log-log plot of intensity ratios versus concentration concentrations that fall significantly above the straight line
arenotaffectedbythecontrastofthephotographicemulsionor establishedbythelowestandoneofthehigherconcentrations,
the conditions of development. When using a direct-reading this is a clear indication of probable interference from another
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Please contact ASTM International (www.astm.org) for the latest information.
´1
E 158 – 86 (1996)
element. The distance above the line is a measure of the 6.5.5 Instrumental changes that result in a proportional
amount of interference. change
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.